How exactly did Einstein come up with his theory of general relativity? Although I’ve read several books on general relativity and felt confident to say that I understand the fundamentals, I only recently understood where exactly it came from.

So here’s a hopefully coherent story of how we can invent Einstein’s theory from scratch.

Why should accelerating frames be special?

The first thing we need to wonder about is the notion “acceleration”. While no one doubts that there is no difference between frames of reference that move with constant speed relative to each other, accelerating frames are special. In a soundproof, perfectly smooth moving train without windows, there is no way to tell if the train moves at all. However, we notice immediately when the train accelerates. A glass of water is indistinguishable in a perfectly smooth moving train from a glass of water in a standing train. However if the train accelerates rapidly, the water spills over.

The equivalence of frames that move with constant velocity relative to each other is known as Galilean relativity and was successfully extended by Einstein to his theory of special relativity. The additional thing that special relativity takes into account is that the speed of light has the same value for all observers.

Now, Einstein was dissatisfied by the special role of accelerating frames. Why should they be special? What makes them special? Is there any way to put them on an equal footing to all other frames?

Galilean relativity and Einstein’s relativity put all frames that move with constant velocity relative to each other on an equal footing. That’s a big unification. However, the unification is not complete as long as accelerating frames are special.

To understand what defines acceleration after all and what makes it special, we need to consider some extreme situations.

For example, let’s imagine an infinite, completely empty universe with just one observer somewhere inside. Is he stationary? What if he starts spinning? Would he feel dizzy? How could he tell that he spins at all? What if the universe starts spinning around him? Would he feel dizzy? is there any way to distinguish these scenarios?

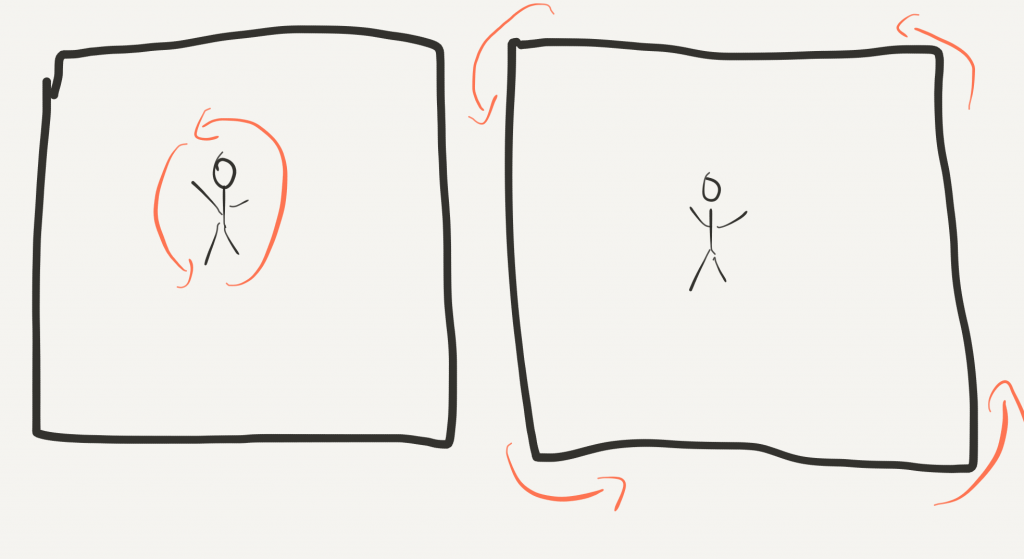
There are only two answers. Either there is an absolute frame of reference, let’s call it “God’s frame”, or there is no way to distinguish these situations. While many people preferred for a long time the first possibility, the second one is Einstein’s perspective. He was a huge fan of the philosopher Ernst Mach, who argued using many thought experiments that the idea of absolute motion makes no sense.

In special relativity, what one observer calls a moving object, is an object at rest for another observer. There is no way to make an absolute statement of the form “this object is moving!”. In contrast, we can always state absolutely “this object is accelerating”.

However, Einstein’s hope was that it would be equally possible to make acceleration relative somehow. What one observer would call an accelerating object, another would call an object at rest. If this would be possible somehow, the laws of nature would be exactly the same for accelerating observers and observers at rest.

As already mentioned above, there are many good reasons to believe that this is simply not possible. Just take the next train and you’ll see how different accelerating frames are! Einstein was well aware of these obstacles, but he was obsessed by the idea that no frame should be special.

To move forward, we need to find out what makes accelerated frames special. Einstein, as any student of physics, learned in his mechanics lectures that in accelerating frames we need to take care of additional forces, called “fictitious forces”. These additional forces take care of the anomalous movement of objects in accelerating frames. A special feature of fictitious forces is that they are proportional to the mass of the object in question. While thousands of students learned these things every year, no one paid special attention to them. This is no wonder. Calculations in accelerated frames are extremely complicated and you can always simply choose another observer that isn’t accelerating.

However, Einstein was obsessed with his idea that no frame should be special and somehow at the right moment, these distant memories of what he learned in his mechanics’ course started popping up.

Another thing every student of physics learns is Newton’s formula $ m M /d^2$ that describes the gravitational force between two objects of mass $m$ and $M$ that are separated by a distance $d$. This law is completely analogous to Coulomb’s law $qQ/d^2$ that describes the electric force between two charged objects. The only difference is that gravity is always attractive, while the electric force can also be repelling. (Like charges repel each other, while unlike charges attract each other)

Remembering these two facts about accelerating frames and gravity, Einstein’s thought process could have been as follows:

“Fictitious forces are proportional to the mass of the object in question … The gravitational force is equally proportional to the mass of the object in question … Gravity reminds me of a fictitious force… Maybe gravity is a fictitious force!”

To explore this possibility, let’s imagine a spacetime somewhere in the universe far away from anything else. Usually, the astronauts in a spaceship float around of the spaceship aren’t accelerating. There is no way to call one of the walls the floor and another one the ceiling.

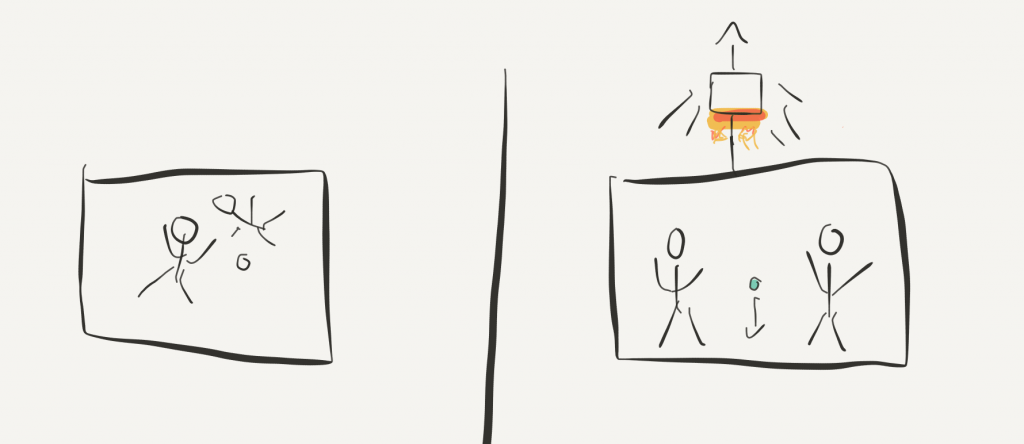
Now, what happens if another spaceship starts pulling the original spaceship? Immediately there is an “up” and a “down”. The passengers of the spaceship get pushed towards one of the walls. This wall suddenly becomes the floor of the spaceship. If one of the passengers drop an apple it falls to the floor.

For an outside observer, this isn’t surprising. Through the pulling of the second spaceship, the floor is moving towards the floating pencil. This leads to the illusion for the passengers inside the original spaceship that the pencil falls to the floor.

If there is no window in the original spaceship, there is no possibility for the astronauts to tell if they are sitting still on some planet or if they are accelerating. If their spaceship sits on a planet the pencil and the passengers themselves would be equally pulled to the floor, however in this case through gravity.

Even if we try to exploit some special possibility of gravity, there is no way to distinguish these situations. For example, a bowling ball and a pencil that is released from the same height would hit the floor at the same moment. This is what Galileo demonstrated for gravity, by throwing things down the Tower of Pisa. For an observer outside of the original spacetime, this fact would be by no means mysterious. The floor simply moves constantly towards the floating bowling ball and pencil. Hence, the floor touches the pencil and the bowling ball at exactly the same moment.

An outside observer would call the force that pushes thing to the floor in the original spacetime a fictitious force. It is merely a result of the floor moving towards the floating objects. However, for the passengers inside the spaceship, the force would be very real. They experience a real floor and a real ceiling and things really fall down if you let them drop. Without getting an outside view, it would be impossible for them to distinguish this fictitious force caused by the acceleration of their spaceship, from the force we call gravity. They can’t distinguish between acceleration and sitting at rest in an appropriate gravitational field.

This is crazy. Consider where we started. We were certain that accelerating frames are easily distinguishable. But now we find ourselves in a situation where we can’t find any difference between an accelerating frame and a stationary frame in a gravitational field.

Of course, the situation is only indistinguishable if the acceleration has a precise value that mimics the effect of the gravitational field. If you want to mimic the earth’s gravitational field, you need to accelerate quicker, than if you want to mimic the weaker gravitational field of the moon.

By remembering a simple fact about fictitious forces, Einstein was able to expand his principle of relativity even further. Now, even accelerating frames aren’t that special anymore.

This observation that accelerated frames are indistinguishable from a resting frame immersed in a gravitational field is called, well, the principle of equivalence.

The Principle of Equivalence

To bring this point really home, let’s imagine another situation. Instead of a spaceship somewhere in the middle of nowhere, let’s consider a spaceship floating 100 kilometers above the earth. The spaceship is pulled down by the earth’s gravitational field, but for the moment let’s imagine the spaceship is stationary. In this situation, the astronauts in the spaceship are able to distinguish “up” and “down” without problems. A pencil falls down, thanks to the earth’s gravitational field.

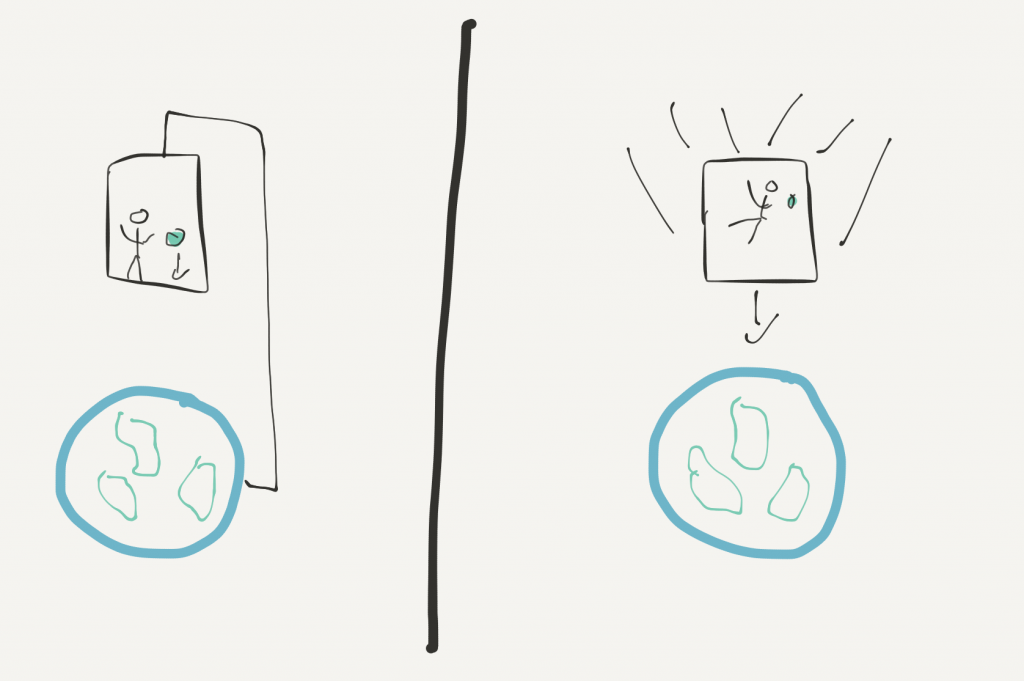
Then suddenly the spaceship is released from whatever holds it still 100 kilometers above the earth. What happens now? Of course, the spaceship starts falling down, i.e. moves towards the earth. At the same time the notions “up” and “down” start losing their meaning for the astronauts inside the spaceship. Everything inside the spaceship falls down towards the earth with exactly the same speed. This property of gravity was demonstrated by Galileo through his famous experiments at the Tower of Pisa. Thus, everything inside the spaceship starts floating. They experience zero gravity. For them, without the possibility to look outside of their spaceship, there is no gravitational field and nothing is falling down.

Therefore, gravity is nothing absolute. While for some observers there is a gravitational field, for the free-falling observers inside the spaceship there is none. If we want, we can therefore always consider some frame where there is no gravity at all! The gravitational force vanishes completely inside the free-falling spaceship. In contrast, an observer standing on earth would describe the spaceship by taking the earth’s gravitational field into account. To such an observer everything falls down because of this gravitational field. However, for the astronauts inside the spaceship, nothing is falling.

This situation is exactly the reversed situation to our first imaginary scenario. There we considered a spaceship somewhere in the middle of nowhere, where there was no gravitational field. Then the spaceship got pulled by another spaceship and suddenly the situation inside the original spaceship was as if they were immersed in a gravitational field. In our second imaginary situation, we started with a spaceship immersed in a gravitational field. However, all effects of this gravitational field vanish immediately when the spaceship starts falling freely towards the earth. Gravity has no absolute meaning. For some frames of reference there is gravity, for others, there isn’t.

The final Punchline

So far, we only considered linear acceleration. In both examples above the spaceship moved in a fixed direction with varying speed. However, not only when the magnitude of speed changes we have acceleration but also when an object changes direction. Another kind of accelerated frame is rotating frames.

The simplest kind of system we can consider is a disk that spins with a fixed number of revolutions per second. Each point on the disk undergoes a change in direction at every instant and is, therefore, accelerating all the time.

To understand a spinning disk we need to remember one of the most curious properties of special relativity: length contraction. The length of an object is smaller for some observer who moves with some velocity relative to the object than the length measured by some observer for whom the object is at rest.

Each point on our spinning disk moves round and round, but not in and out. Thus, according to special relativity, there is length contraction along the circumference, but none along the radius. Thus, when we measure the circumference of a spinning disk, we measure a different value than an observer who sits on the spinning disk. For the observer sitting on the spinning disk, the disk is at rest and hence no length contraction happens. However, we agree with this observer on the diameter of the disk, since even for us there is no radial movement of the disk.

The formula everyone learns in school for the relation of the radius $r$ to the circumference $C$ of a circle is:

$$ C = 2 \pi r . $$

Thus, the ratio of the circumference and radius that the observer on the disk, for whom the disk is at rest measures is $ C/r = 2 \pi$. For us outside observers, the disk spins and therefore there is length contraction along the circumference. Therefore, what we measure is not the same: $ C/r \neq 2 \pi$! This crazy result was known for some time as “Ehrenfest’s paradox”.

Once more Einstein understood what was going on here by remembering something he learned in a seminar. In a seminar about the geometry of two-dimensional curved surfaces, he learned that in non-Euclidean geometry the ratio $ C/r$ needs not necessarily be $2 \pi$. Depending on the surface we are considering the ratio can be any value.

The simplest example to understand this is a sphere. Let’s consider the ratio $C/r$ for the equator of a sphere, say the earth. The circumference is some number $C= C_E$. The radius of this circle is the distance from any point on the equator all the way up to the north pole. For a perfect sphere, the length of such a line is exactly one-half equator: $r= C_E /2$. Therefore, the ratio $C/r$ for a circle on a sphere is not $2 \pi$, but $C/r= C_E /(C_E / 2) = 2$!

Einstein remembered this property of curved surfaces and connected it with the seeming paradox situation concerning the $C/r$ ratio of a spinning disk. The mathematics of how to describe things on curved surfaces was at this time already developed by Gauss and Riemann. Einstein’s idea was to borrow these mathematical tools to describe what is going on in accelerating frames. Thanks to his equivalence principle accelerating frames are equivalent to resting frames in a gravitational field. Hence he noted that he could use the mathematics of Gauss and Riemann to describe gravity.

The Einstein Equation

Now, all we have to do is write down the correct equation that describes the idea “gravity = curved spacetime” mathematically. Einstein needed 6 years to discover the correct formula, but nowadays with the power of hindsight, the derivation is relatively straight-forward.

What causes gravity is mass, and thanks to Einstein’s famous formula $E = m c^2$, we know that equally energy causes gravity. Thus, at one side of our equation, we must have something describe the “charge” of gravity, i.e. energy. In mathematical terms, the “charge” of gravity is described by the energy-momentum tensor $ T_{\mu \nu}$.

As a first step towards our equation, we must now remember one of the most important laws of physics: the conservation of energy and momentum. In mathematical terms this conservation law is expressed as

\begin{equation} \partial^\mu T_{\mu \nu} = 0. \end{equation}

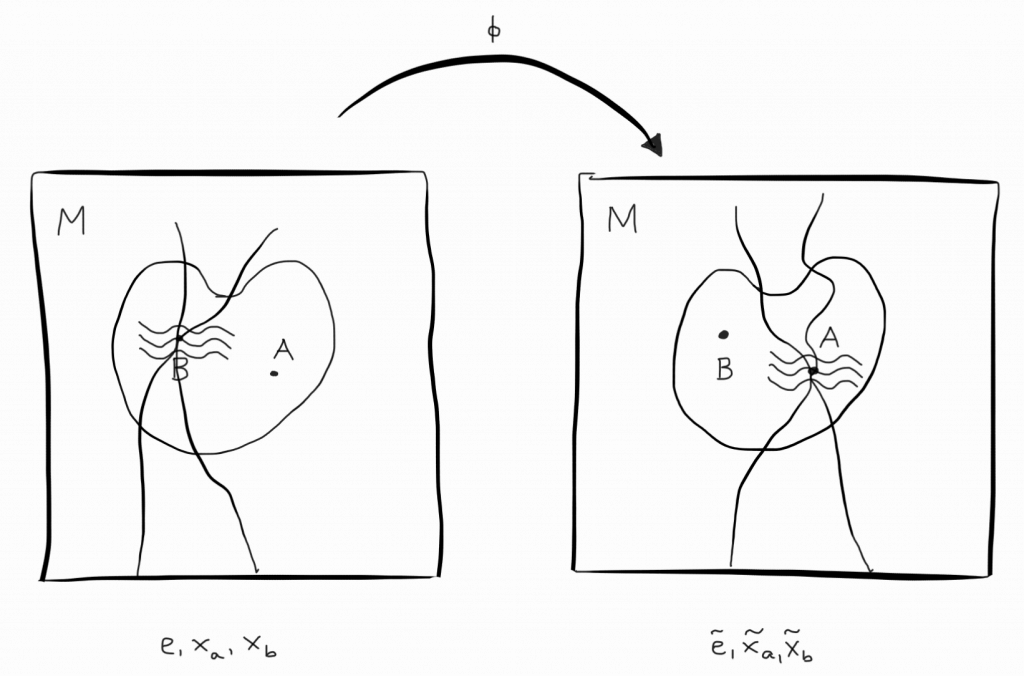
Next, we need something to describe curvature mathematically. This is what makes general relativity computationally very demanding. The most important object in this context is the metric. Metrics are mathematical objects that enable us to compute the distance between two points. In a curved space, the distance between two points is different than in a flat space as illustrated the following figure: (Geodesic)

Therefore metrics will play a very important role when thinking about curvature in mathematical terms.

Having talked about this, we are ready to “derive” the Einstein equation. It turns out that there is exactly one mathematical object that we can put on the left-hand side: the Einstein tensor $G_{\mu \nu}$. The Einstein tensor is the only divergence-free ($\partial^\mu G_{\mu \nu}=0$) function of the metric $g_{\mu\nu}$ and at most its first and second partial derivative. Therefore, the Einstein tensor may be very complicated, but it’s the only object we are allowed to write on the left-hand side describing curvature. This follows, because we can conclude from
\begin{equation} T_{\mu \nu} = C G_{\mu \nu} \quad \text{ that } \quad \partial^\mu T_{\mu \nu} = 0 \rightarrow \partial^\mu G_{\mu \nu} = 0\end{equation}
must hold, too. The Einstein tensor is a second rank tensor and has exactly this property. Second rank tensor means two indices $\mu \nu$, which is a necessary requirement, because $T_{\mu \nu}$ on the right-hand side has two indices, too.

The Einstein tensor is defined as a sum of the Ricci Tensor $R_{\mu\nu}$ and the trace of the Ricci tensor, called Ricci scalar $R =R_{\nu}^\nu$
\begin{equation} G_{\mu \nu} = R_{\mu\nu}-\frac{1}{2}Rg_{\mu \nu} \end{equation}
where the Ricci Tensor $R_{\mu\nu}$ is defined in terms of the Christoffel symbols $\Gamma^\mu_{\nu \rho}$

\begin{equation}
R_{\alpha\beta} = \partial_{\rho}{\Gamma^\rho_{\beta\alpha}} – \partial_{\beta}\Gamma^\rho_{\rho\alpha} + \Gamma^\rho_{\rho\lambda} \Gamma^\lambda_{\beta\alpha} – \Gamma^\rho_{\beta\lambda}\Gamma^\lambda_{\rho\alpha} \end{equation}
and the Christoffel Symbols are defined in terms of the metric
\begin{equation}
\Gamma_{\alpha \beta \rho} =\frac12 \left(\frac{\partial g_{\alpha \beta}}{\partial x^\rho} + \frac{\partial g_{\alpha \rho}}{\partial x^\beta} – \frac{\partial g_{\beta \rho}}{\partial x^\alpha} \right) = \frac12\, \left(\partial_{\rho}g_{\alpha \beta} + \partial_{\beta}g_{\alpha \rho} – \partial_{\alpha}g_{\beta \rho}\right). \end{equation}
This can be quite intimidating and shows why computations in general relativity very often need massive computational efforts.

Next, we need to know how things react to such a curved spacetime. What’s the path of an object from A to B in curved spacetime? The first guess is the correct one: An object follows the shortest path between two points in curved spacetime. We can start with a given distribution of energy and mass, which means some $T_{\mu \nu}$, compute the metric or Christoffel symbols with the Einstein equation and then get the trajectory through the \textbf{geodesic equation}
\begin{equation} \label{eq:geodesics}
\frac{d^2x^\lambda }{dt^2} + \Gamma^{\lambda}_{\mu \nu }\frac{dx^\mu }{dt}\frac{dx^\nu }{dt} = 0.
\end{equation}
The geodesic is the locally shortest curve between two points on a manifold. (This is a bit oversimplified, but the correct definition needs some terms from differential geometry we haven’t introduced here.)

That’s it.

My plan is to write next about why this idea “gravity = curvature” is not the really the essence of general relativity. This somewhat controversial statement is something that even Einstein himself only understood after several decades. However, this post is already incredibly long and thus I’ll write another post about this.

To finish this post, here are some recommendations where to read more about Einstein’s theory: 

• To understand Einstein’s equation and thus general relativity better I highly recommend “The Meaning of Einstein’s Equation” by John C. Baez and Emory F. Bunn.
• Another nice and quick introduction is A No-Nonsense Introduction to General Relativity by Sean M. Carroll

My favorite GR textbooks are

•  “Relativity, Gravitation and Cosmology” by Ta-Pei Cheng, which focusses nicely on practical applications and never gets lost in technical details.
• “Einstein Gravity in a Nutshell” by A. Zee, which nicely focusses on questions that are usually troubling for students.