In quantum field theory, we can’t calculate things exactly but instead must use a perturbative approach. This means, we calculate observables in terms of a perturbative series: $\mathcal{O}= \sum_n c_n \alpha^n$.
This approach works amazingly well. The most famous example is the magnetic dipole moment of the electron $a_e \equiv (g – 2)/2$. It was calculated to order $\alpha^5$ in Phys. Rev. Lett. 109, 111807 and this result agrees perfectly with the measured value:
$$a_e(exp) – a_e(theory) = −1.06 \ (0.82) \times 10^{-12}$$
However, there is one thing that seems to cast a dark shadow over this rosy picture: there are good reasons to believe that if we would sum up all the terms in the perturbative series, we wouldn’t get a perfectly accurate result, but instead infinity: $ \sum_n^\infty c_n \alpha^n = \infty$. This is not some esoteric thought but widely believed among experts. For example,
“The only difficulty is that these expansions will at best be asymptotic expansions only; there is no reason to expect a finite radius of convergence.”
G. ‘t Hooft, “Quantum Field Theory for Elementary Particles. Is quantum field theory a theory?”, 1984
“Quantum field theoretic divergences arise in several ways. First of all, there is the lack of convergence of the perturbation series, which at best is an asymptotic series.”
R. Jackiw, “The Unreasonable Effectiveness of Quantum Field Theory”, 1996
“It has been known for a long time that the perturbation expansions in QED and QCD, after renormalization, are not convergent series.”
G. Altarelli, “Introduction to Renormalons”, 1995
And this is really just a small sample of people you could quote.
This is puzzling, because as is “well known”:
“Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.”
Niels Hendrik Abel, 1828
In this sense, the perturbation series in QFT is an “invention of the devil” and we need to wonder $ \sum_n^\infty c_n \alpha^n = \infty \quad \Rightarrow $ ???
But, of course, before we deal with that, we need to talk about why this divergence of the perturbation series is so widely believed.
Does the perturbation series converge?
$$\mathcal{O}(\alpha)= c_0 + \alpha c_1 + \alpha^2 c_2 + \ldots $$
To answer this question, Dyson already in 1952 published a paper titled “Divergence of perturbation theory in quantum electrodynamics” in which he put forward the clever idea to exploit one of the basic theorems of analysis.
The theorem is: If $0 < r < \infty$, the series converges absolutely for every real number $\alpha$ such that $|\alpha|<r$ and diverges outside of this radius. Here, $r$ is called the radius of convergence and is a non-negative real number or $\infty$ such that the series converges if $|\alpha| < r$.
The important subtlety implied by this theorem that Dyson focused on is that if the radius of convergence is finite $\neq 0$, according to the theorem, the series would also converge for small negative $\alpha$.
In other words: If a series converges it always converges on a disk!
Dyson idea to answer the question “Does the perturbation series converge?” is that we should check if the theory makes sense for a negative value of the coupling constant $\alpha$. If we can argue somehow that the theory explodes for any negative $\alpha$ then we know immediately that $r =0$ and therefore that the perturbation series diverges.
Does QED make sense with negative $\alpha$?
Before we discuss Dyson’s argument why the theory explodes for negative $\alpha$ in detail, here is a short summary of the main line of thought:
We consider a “fictitious world” with negative $\alpha$. In such a world, equal charges attract each other, and opposite charges repel each other.
With some further thought, we will discuss in a moment, this means that the energy is no longer bounded from below. Therefore, in a world with negative $\alpha$, there is no stable ground state.
For our perturbation series, this means, that it is non-analytic around $\alpha = 0$. In other words, electrodynamics with negative $\alpha$, cannot be described by well-defined analytic functions. Therefore we can conclude that the radius of convergence is zero $r=0$, which implies that the perturbation series in QFT diverges also for a positive value of $\alpha$.
In other words, the physics as soon as $\alpha$ becomes negative is so dramatically different that we expect a singularity at $\alpha =0$. Consequently, there doesn’t exist a convergent perturbation series.
After this short summary, let’s discuss how this comes about in more detail.
The important change as soon as $\alpha$ becomes negative is that equal charges start to attract each other. In the “normal” world with positive $\alpha$ a pair of, say, electron and positron that are created from the vacuum attract each other and therefore annihilate immediately, In a world with negative $\alpha$ they repel each other and therefore fly away from each other instead of annihilating.
This means, the naive empty vacuum state starts to fill up with electrons and positrons when $\alpha$ is negative.
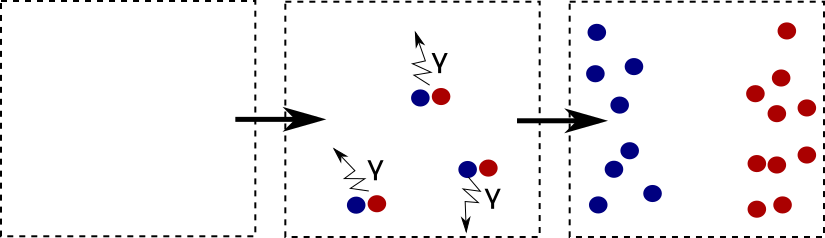
Wait, is this energetically possible? What’s the energy of this new state full of electrons and positrons?
To answer this question, let’s consider a ball with radius $R$ full of electrons and calculate its energy content.
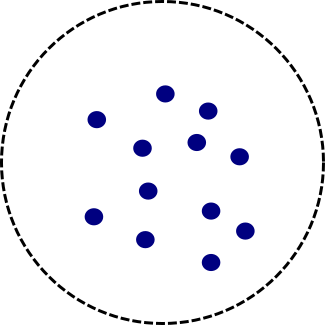
On the one hand, we have the positive rest + kinetic energy, which are proportional to the number of particles inside the ball $\propto N$.
On the other hand, we have the negative potential energy, which is given by the usual formula for a Coulomb potential $\propto N^2 R^{-1}$.
To compare them with each other, we need to know the number of electrons inside the ball. According to the Pauli principle, this number is proportional to the volume of the ball and therefore we conclude $\propto V \propto R^3 \propto N$.
Therefore, the positive part of the energy is proportional to $R^3$, and the negative energy to $\propto N^2 R^{-1} \propto R^5$. The negative part wins.
The total energy of the electrons inside the ball is negative. Most disturbingly the energy is unbounded from below and becomes arbitrarily negative as we make the ball bigger: $R,N \to \infty$.
Take note that this is only the case in our fictitious world with negative $\alpha$. In our normal world with positive $\alpha$, opposite charges attract each other and this repulsion sets a lower bound on the energy. The analogous situation to the ball above in our fictitious world is a ball full of electron-positron pairs.
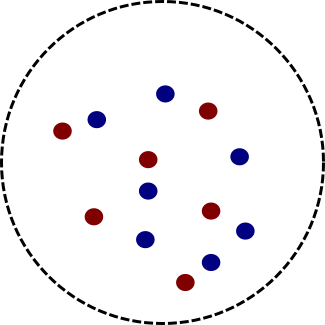
The crucial thing is now that we can’t lower the energy indefinitely because when we try to group more and more electron-positron pairs together, we necessarily bring electrons close to other electrons and positrons close to other positrons. These equal charged particles repel each other in our normal world and this sets a lower bound on the energy.
So, to conclude: In contrast to our normal world with positive $\alpha$, in our fictitious world with negative $\alpha$, a bound state of many electrons or positrons has a large negative energy. This means that our energy isn’t bounded from below because it can become arbitrarily negative. The most dramatic effect of this is what happens to the ground state in such a world, as already mentioned above. If we would start with a naive vacuum with no particles, it would spontaneously turn into a state with lots of electrons on one side and lots of positrons on the other side.
“Although this state is separated from the usual vacuum by a high potential barrier (of the order of the rest energy of the 2N particles being created), quantum-mechanical tunneling from the vacuum to the pathological state would be allowed, and would lead to an explosive disintegration of the vacuum by spontaneous polarization.”
S. Adler, “Short-Distance Behavior of Quantum Electrodynamics and an Eigenvalue Condition for $\alpha$”, 1972

This process would never stop. When the vacuum state isn’t stable against decay, no state is. Therefore, in a world with a negative coupling constant, every state could decay into pairs of electrons and positrons indefinitely.
So, as claimed earlier, physics truly becomes dramatically different as soon as the coupling constant becomes negative.
“This instability means that electrodynamics with negative $\alpha$, cannot be described by well-defined analytic functions; hence the perturbation series of electrodynamics must have zero radius of convergence.”
Adler, “Short-Distance Behavior of Quantum Electrodynamics and an Eigenvalue Condition for $\alpha$”, 1972
For example, an observable like the magnetic dipole moment of the electron will have completely different value as soon as $\alpha$ becomes negative. Or it is even possible that such a property wouldn’t even make any sense in a world with negative $\alpha$.
This leads us to the conclusion that we have a singularity at $\alpha=0$, which means we can’t write down a convergent perturbation series for observables.
It is certainly fun to think about a world with a negative coupling constant and Dyson’s argument makes a lot of sense. Nevertheless, it is important to keep in mind that this is by no means a proof. It’s just a heuristic argument, but neither general nor rigorous.
Yet, many people are convinced by it and further arguments that point in the same direction.
One such further argument is the observation, already made in 1952 and later refined by Bender and Wu that the number of Feynman diagrams grows rapidly at higher orders of perturbation theory.
At order $n$, we get $n!$ Feynman diagrams. For our sum $\sum_n^\infty c_n \alpha^n$ this means that $c_n \propto n!$. Thus, no matter how small $\alpha$ is, at some order $N$ the factor $N!$ wins.
Now that I have hopefully convinced you that $ \sum_n^\infty c_n \alpha^n = \infty$, we can start asking:
What does $ \sum_n^\infty c_n \alpha^n = \infty$ mean?
The best way to understand what $ \sum_n^\infty c_n \alpha^n = \infty$ really means and how we can nevertheless get good predictions out of the perturbation series is to consider toy models.
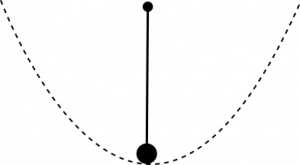
As already mentioned in my third post about the QCD vacuum, one of my favorite toy models is the quantum pendulum. It is the perfect toy model to understand the structure of the QCD vacuum and the electroweak vacuum and will be now invaluable again.
The Schrödinger equation for the quantum pendulum is
$$ – \frac{d^2 \psi}{d x^2} + g(1-cos x) \psi = E \psi . $$
We want to calculate things explicitly and therefore consider a closely related, simpler model and will come back to the full pendulum later. For small motions of the pendulum, we can approximate the potential ( $\cos(x) \approx 1-x^2/2+x^4/4! – \ldots$) of the quantum pendulum and end up with the Schrödinger equation for the anharmonic oscillator
$$ – \frac{d^2 \psi}{d x^2} – (x^2+ g x^4 )\psi = E \psi . $$
Now, the first thing we can do with this toy model is to understand Dyson’s argument from another perspective.
The potential of the anharmonic oscillator is $ V= x^2+ g x^4$ and let’s say we want to calculate the energy levels by using the usual quantum mechanical perturbation theory $E(g) = \sum_n c_n g^n $. (More precisely: The energy levels of the harmonic oscillator are well known and we are using the Rayleigh-Schrödinger perturbation theory to calculate corrections to them which come from the anharmonic term $\propto x^4$ in the potential. )
For positive values of $g$ the potential is quite boring and looks almost like for the harmonic oscillator. However, for negative values of $g$ the situation becomes much more interesting.
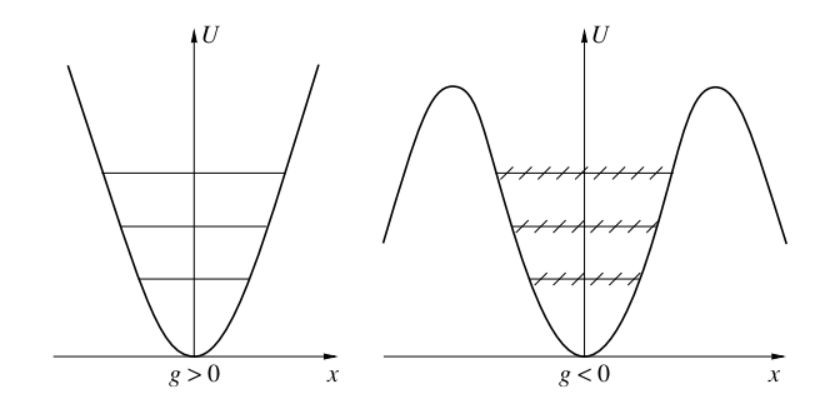
The energy is no longer bounded from below. The states inside the potential are no longer stable but can decay indefinitely by tunneling through the potential barrier. This is exactly the same situation that we discussed earlier for QED with negative $\alpha$.
Thus, according to Dyson’s argument, we suspect that the perturbation series for the energy levels is not convergent.
This was confirmed by Bender and Wu, who treated the “anharmonic oscillator to order 150 in perturbation theory“. (Phys. Rev. 184, 1231 (1969); Phys. Rev. D 7, 1620 (1973))
We can already see from the first terms in the perturbation theory how the series explodes:
$$ \rightarrow E_0 \propto \frac{1}{2} + \frac{3}{4}g – \frac{21}{8}g^2 + \frac{333}{16}g^3 + \ldots $$
This gives further support to Dyson’s conjecture that a dramatically different physics for negative values of the coupling constant means that the perturbation theory does not converge.
Yet, the story of this toy model does not end here. There is much more we can do with it.
The Anharmonic Oscillator in “QFT”
Let’s have a look how we would treat the anharmonic oscillator in quantum field theory. (This example is adapted from the excellent https://arxiv.org/abs/1201.2714). For this purpose, we consider the following “action” integral
$$\mathcal{Z}(g) = \int_{-\infty}^\infty \mathrm{d}x \mathrm{e}^{-x^2-g x^4} .$$
The cool thing is now that we can compute for this toy model the exact answer, for example, using Mathematica. Then, in a second step we can treat the same integral was we usually do in QFT and then compare the perturbative result with the exact result. Then in the last step, we can understand at what order and why the perturbation series diverges.
The full, exact solution isn’t pretty, but no problem for Mathematica:
$$ \mathcal{Z}(g) = \frac{\mathrm{e}^{\frac{1}{8g}}K_{1/4}(1/8g}{2 \sqrt{g}}, $$
where $K_n$ denotes modified Bessel function of the second kind. This solution yields a finite positive number for each value $g$.
Next, we do what we usually do in QFT. We split the “kinetic” and the “interaction” part and expand the interaction part as a power series
\begin{align}
\mathcal{Z}(g) &= \int_{-\infty}^\infty \mathrm{d}x \mathrm{e}^{-x^2-g x^4} = \int_{-\infty}^\infty \mathrm{d}x \mathrm{e}^{-x^2} \sum_{k=0}^\infty \frac{(-gx^4)^k}{k!} \notag \\
& \text{“}= \text{“} \sum_{k=0}^\infty \int_{-\infty}^\infty \mathrm{d}x \mathrm{e}^{-x^2} \frac{(-gx^4)^k}{k!} \notag
\end{align}
Take note that the exchange of sum and integral is the “root of all evil”, but necessary to interpret the theory in terms of a power series of Feynman diagrams. That’s why the last equal sign is put in quotes. (This exchange is actually a “forbidden” step that changes the behaviour at $\pm \infty$. )
So, with this approach to what extend can we get a good approximation?
Using a bit of algebra, we can solve the polyonimian times Gaussian integral and get
\begin{align}
\mathcal{Z}(g) & \text{“}= \text{“} \sum_{k=0}^\infty \int_{-\infty}^\infty \mathrm{d}x \mathrm{e}^{-x^2} \frac{(-gx^4)^k}{k!} \notag \\
&= \sum_{k=0}^\infty \sqrt{\pi} \frac{(-g)^k (4k)!}{2^{4k}(2k)! k!}
\end{align}
This perturbative answer is a series that diverges! (For more details, see the excellent detailed discussion in https://arxiv.org/abs/1201.2714)
Is this perturbative answer, although divergent, useful anyway?
Let’s have a look.
The thing is that in QFT we can only compute a finite number of Feynman diagrams. This means we can only evaluate the first few terms of the perturbation series. Thus we consider the “truncated” series, instead of the complete series, which simply means we stop at some finite order $N$:
$$ \Rightarrow \text{Truncated Series: } \mathcal{Z}_N(g) = \sum_{k=0}^N \sqrt{\pi} \frac{(-g)^k (4k)!}{2^{4k}(2k)! k!} $$
For definiteness let’s choose some value for the coupling constant, say $g=\frac{1}{50}$. How good is the perturbative answer from the truncated series compared to the full exact answer?
\begin{align}
\text{Exact: } \mathcal{Z}(1/50) &= 1.7478812\ldots \notag \\
\text{Perturbatively: } \mathcal{Z}_5(1/50) &= 1.7478728\ldots \notag \\
\mathcal{Z}_{10}(1/50) &= 1.7478818\ldots \notag
\end{align}
This is astoundingly good! The complete series is divergent, which means if we would sum up all the terms, we would get infinity. Nevertheless, if we only consider the first
few terms, we get an excellent approximation of the correct answer!
This behavior can be understood nicely by a plot
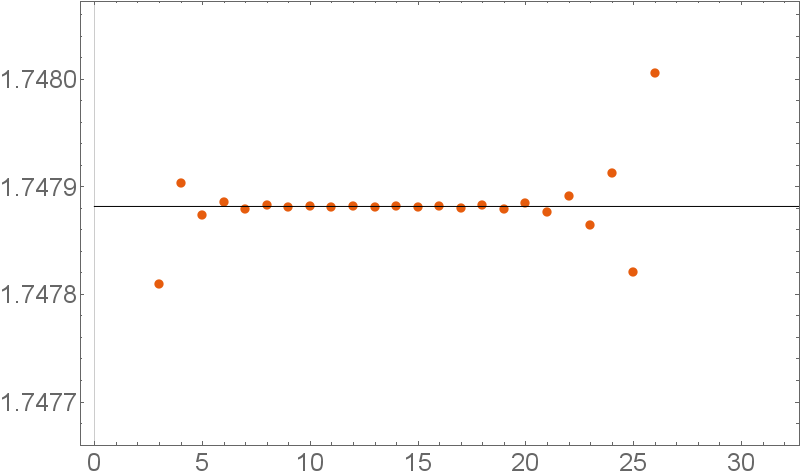
The first few terms are okay, then the approximation becomes really good, but at some point, the perturbative answer explodes. A series that behaves like this is known as an asymptotic series.
So now, the question we need to answer is:
When and why does the series diverge?
Again, I will give you a short summary of the answer first, and afterward discuss it in more detail.
The reason that the series explodes at some point is that a perturbative treatment in terms of a Taylor series misses completely factors of the form $ \mathrm{e}^{-c/g} \sim 0 + 0 g + 0 g^2 + \ldots $. The Taylor expansion of such a factor yields zero at all order, although the function obviously isn’t zero. This is a severe limitation of the usual perturbative approach.
You may wonder, why we should care about such funny looking factors. The thing is that tunneling effects in a quantum theory are described precisely by such factors! Remember, for example, the famous quantum mechanical answer of a particle that encounters a potential barrier. It will tunnel through the barrier, although classically forbidden. Inside the potential barrier, we don’t get an oscillating wave function, but instead, an exponentially damping, described by factors of the form $ \mathrm{e}^{-c/g}$.
To summarize: Our perturbative approach misses tunneling effects completely and this is why our perturbation series explodes!
We will see in a moment that this means that the divergence starts around order $N=\mathcal{O}(1/g)$. For example, in QED the perturbative approach is expected to work up to order 137.
We can understand this, by going back to our toy model. Have a look again at the quantum pendulum.

Usually, we consider small oscillations around the ground state, which means low energy states. However in a quantum theory, even at low energies, the pendulum can do something completely different. It can rotate once around its suspension. As it classically does not have the energy to do this, we have here a tunneling phenomenon. This kind of effect is what our usual perturbative approach misses completely and this is why the perturbation series explodes.
After this heuristic discussion, let’s have a more mathematical look how this comes about.
There is a third method, how we can treat our integral $\mathcal{Z}(g) = \int_{-\infty}^\infty \mathrm{d}x \ \mathrm{e}^{-x^2-g x^4}$. This third method is known as the method of steepest descend and it shows nicely what goes wrong with when we use the usual perturbative method.
First, we substitute $x^2\equiv \frac{u^2}{g}$ and then have
$$\mathcal{Z}(g) = \int_{-\infty}^\infty \mathrm{d}x \ \mathrm{e}^{-x^2-g x^4} = \frac{1}{\sqrt{g}} \int_{-\infty}^\infty \mathrm{d}u \ \mathrm{e}^{- \frac{u^2 + u^4}{g}}$$
Now, we deal with small values of the coupling $g$ and thus the integrand is large. The crucial idea behind the method of steepest descend is that the main contributions to the integral come from the extrema of the integrand $\phi(u)\equiv u^2+u^4$.
As usual, we can calculate the extrema by solving $\phi'(u_0) =0$. Take note that in QFT these extrema of our action integrand are simply the solutions to the equations of motion! (This is how we calculate the equations of motion: we look for extrema of the action. This means, $\phi'(u_0) =0$ are in QFT simply our equations of motion and the solutions $u_0$ are solutions of the equations of motion.
To approximate the integral, we then expand the integrand around these extrema. In our example, the extrema are $u=0$ an $u=\pm i/\sqrt{2}$. (For more details, see https://arxiv.org/abs/1201.2714)
This method tells us exactly what goes wrong in the usual approach. The standard perturbation theory corresponds to the expansion around $u=0$.
The other extrema yield contributions $\propto \mathrm{e}^{-\frac{1}{4g}}$ $\rightarrow$ and as already discussed earlier, these are missed completely by a Taylor series around $g=0$.
With this explicit result, we can calculate when these “non-perturbative” contributions become important.
This question in mathematical terms is: When is $\mathrm{e}^{-\frac{1}{4g}} \approx g^k $?
First, we use the log on both sides, which yields the question: When is $-\frac{1}{4g} \approx k \ \mathrm{ln}(g) $?
Now, if we have a look at some explicit numbers: $ \mathrm{ln}(1/50)\approx -3.9$, $ \mathrm{ln}(1/100)\approx -4.6$, $ \mathrm{ln}(1/150)\approx -5$, we see that the answer is: for $ k \approx \frac{1}{g}$!
Thus, as claimed earlier, the nonperturbative effects that are missed by the Taylor expansion treatment become important at order $\approx \frac{1}{g}$ and this is exactly where our perturbation series stops to make sense.
(For a nice discussion of this method of steepest descent, see page 2 here )
Before we summarize what we have found out and learned here there is one last thing.
One Last Thing
There is an amusing empirical rule related to such asymptotic series:
“(Carrier’s Rule). Divergent series converge faster than convergent
series because they don’t have to converge.” from The Devil’s Invention: Asymptotic, Superasymptotic and Hyperasymptotic Series by John P. Boyd
The thing is that convergence is a concept relating to the behavior at $n \to \infty$. This is not what we are really interested in. We want a good approximation by calculating just a few terms of the perturbation series, not all of them.
This kind of behavior is often observed in divergent series. They often yield good approximation at a low order, which, in contrast, is unusual for convergent power series. This is a numerical, empirical statement that was found in many explicit examples, see: Bender, C. M., and Orszag, S. A.: Advanced Mathematical Methods for Scientists and Engineers, McGraw-Hill, New York, 1978, p. 594
Thus, instead of Abel’s perspective
“Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.“
we should prefer Heaviside’s attitude
“The series is divergent; therefore we may be able to do something with it“
Summary, Conclusions, and Outlook
The thing to take away is nicely summarized by the following picture adapted from a presentation by Aleksey Cherman:
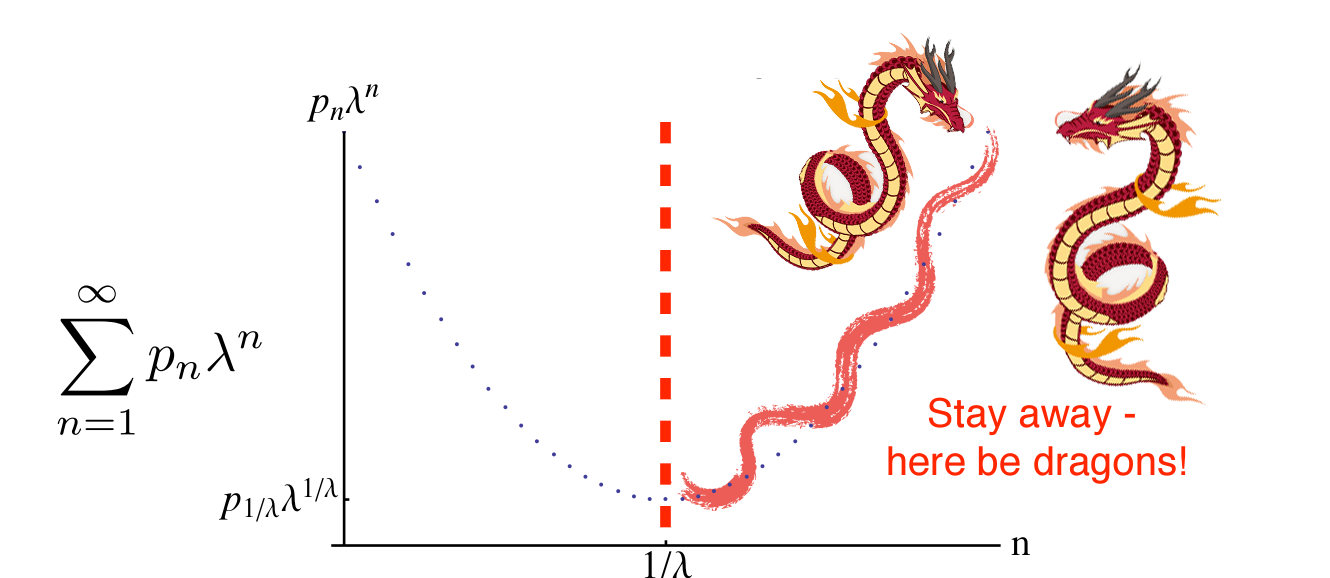
The perturbation series in QFT diverge $\sum_n^\infty c_n g^n =\infty$, but are expected to yield meaningful results up to order $N=\mathcal{O}(1/g)$.
This observation is a great reminder that perturbative Feynman diagrams don’t tell the whole story: tunneling effect, which is proportional to $\mathrm{e}^{1/g}$ are missed completely.
Dyson published his argument in 1952 so all this is known for a long time.
However, there is still a lot of research going on.
One concept people talk about all the time when it comes to this is Borel summation. This is a cool mathematical trick to improve the convergence of divergent series. For the anharmonic oscillator, this works perfectly. By performing a Borel transformation, we can tame the divergence. However, in realistic quantum field theoretical examples this does not work.
The main reason is singularities of the Borel sum. One source of these singularities are the tunneling effects we already talked about. However, much more severe are singularities coming from so-called “renormalons”. This word is used to describe the singularities coming from the renormalization procedure and thus in some sense from the running of the coupling constants.
An active field of research in this direction is “resurgence theory“. People working on this try to use a more general perturbation ansatz
$$\mathcal{O}= \sum_n c_n^{(0)} \alpha^n + \sum_i \mathrm{e}^{S_i/g} \sum_n c_n^{(i)} \alpha^n $$
called a trans-series expansion. The crucial thing is, of course, that they explicitly include the factors $\mathrm{e}^{S_i/g}$ that are missed by the usual ansatz. Thus, in some sense they try to describe “non-perturbative” effects with a new perturbation series.
At the other end of the spectrum are people working on completely non-perturbative results for observables. The most famous example is the amplituhedron, which was proposed a few years ago. This is a geometric object and the people working on it hope that it paves the way to a “nice general solution which would provide all-loop order results.” (J. Trnka)
PS: Many thanks to Marcel Köpke who spotted several typos in the original version.