“Nature is a collective idea, and, though its essence exist in each individual of the species, can never in its perfection inhabit a single object.” ―Henry Fuseli
I recently came across a WIRED story titled “There’s no one way to explain how flying works”. The author published a video in which he explained how airplanes fly. Afterward, he got attacked in the comments because he didn’t mention “Bernoulli’s principle”, which is the conventional way to explain how flying works.
Was his explanation wrong? No, as he emphasizes himself in the follow-up article mentioned above.
So is the conventional “Bernoulli’s principle” explanation wrong? Again, the answer is no.
It’s not just for flying that there are lots of absolutely equally valid ways to explain something. In fact, such a situation is more common than otherwise.
The futility of psychology in economics
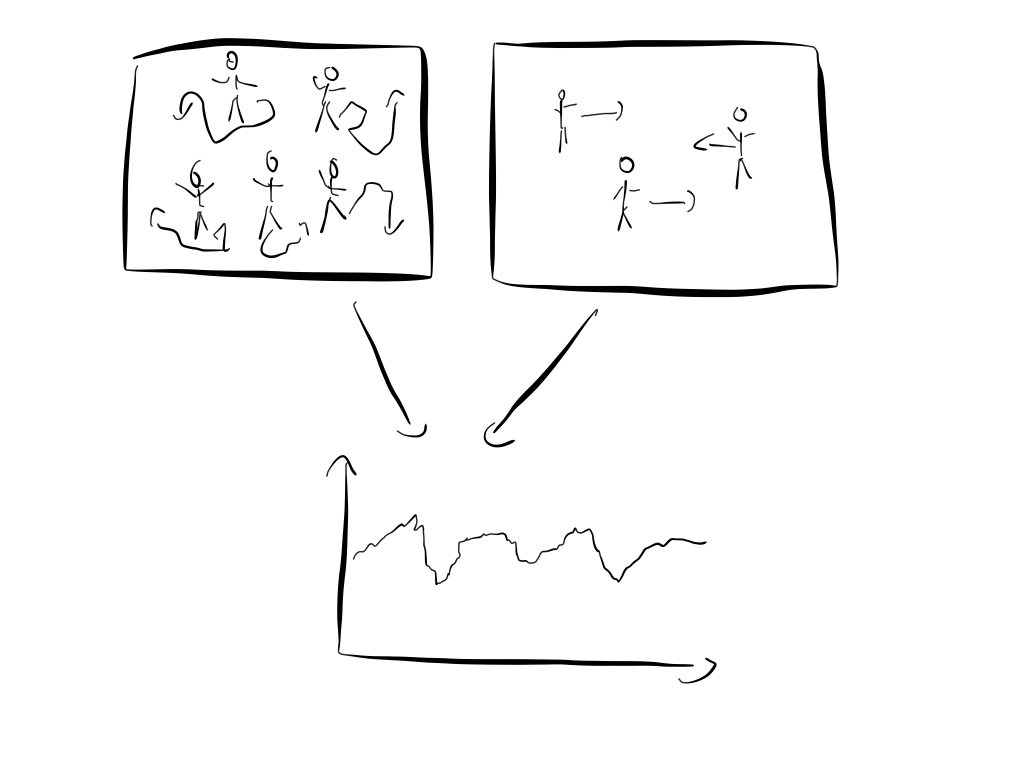
Another good example is economics. Economists try to produce theories that describe the behavior of large groups of people. In this case, the individual humans are the fundamental building blocks and a more fundamental theory would explain economic phenomena in terms of how humans act in certain situations.
An economic phenomenon that we can observe is that that stock prices move randomly most of the time. How can we explain this?
So let’s say I’m an economist and I propose a model that explains the random behavior of stock prices. My model is stunningly simple: humans are crazy and unpredictable. Everyone does what he feels is right. Some buy because they feel the price is cheap. Others buy because they think the same price is quite high. Humans act randomly and this is why stock prices are random. I call my fundamental model that explains economic phenomena in terms of individual random behavior the theory of the “Homo randomicus”.
This hypothesis certainly makes sense and we can easily test it in experiments. There are numerous experiments that exemplify how irrational humans act most of the time. A famous one is the following “loss aversion” experiment:
Participants were given \$50. Then they were asked if they would rather keep \$30 or flip a coin to decide if they can keep all \$50 or lose it all. The majority decided to avoid gambling and simply keep the \$30.
However, then the experimenters changed the setup a bit. Again the participants were given \$50, but then they were asked the participants if they would rather lose \$20 or flip a coin to decide if they can keep all \$50 or lose it all. This time the majority decided to gamble.
This behavior certainly makes no sense. The rules are exactly the same but only framed differently. The experiment, therefore, proves that humans act irrationally.
So my model makes sense and is backed up by experiments. End of the story right?
Not so fast. Shortly after my proposal another economist comes around and argues that he has a much better model. He argues that humans act perfectly rational all the time and use all the available information to make a decision. In other words that humans act as “Homo oeconomicus”. With a bit of thought it is easy to deduce from this model that stock prices move randomly.
This line of thought was first proposed by Louis Bachelier and you can read a nice excerpt that explains it from the book “The Physics of Wall Street” by James Owen Weatherall by clicking on the box below.
Why stocks move randomly even though people act rational
But why would you ever assume that markets move randomly? Prices go up on good news; they go down on bad news. there’s nothing random about it. Bachelier’s basic assumption, that the likelihood of the price ticking up at a given instant is always equal to the likelihood of its ticking down, is pure bunk. this thought was not lost on Bachelier. As someone intimately familiar with the workings of the Paris exchange, Bachelier knew just how strong an effect information could have on the prices of securities. And looking backward from any instant in time, it is easy to point to good news or bad news and use it to explain how the market moves. But Bachelier was interested in understanding the probabilities of future prices, where you don’t know what the news is going to be. Some future news might be predictable based on things that are already known. After all, gamblers are very good at setting odds on things like sports events and political elections — these can be thought of as predictions of the likelihoods of various outcomes to these chancy events. But how does this predictability factor into market behavior?Bachelier reasoned that any predictable events would already be reflected in the current price of a stock or bond. In other words, if you had reason to think that something would happen in the future that would ultimately make a share of Microsoft worth more — say, that Microsoft would invent a new kind of computer, or would win a major lawsuit — you should be willing to pay more for that Microsoft stock now than someone who didn’t think good things would happen to Microsoft , since you have reason to expect the stock to go up. Information that makes positive future events seem likely pushes prices up now; information that makes negative future events seem likely pushes prices down now.But if this reasoning is right, Bachelier argued, then stock prices must be random. think of what happens when a trade is executed at a given price. this is where the rubber hits the road for a market. A trade means that two people — a buyer and a seller — were able to agree on a price. Both buyer and seller have looked at the available information and have decided how much they think the stock is worth to them, but with an important caveat: the buyer, at least according to Bachelier’s logic, is buying the stock at that price because he or she thinks that in the future the price is likely to go up. the seller, meanwhile, is selling at that price because he or she thinks the price is more likely to go down. taking this argument one step further, if you have a market consisting of many informed investors who are constantly agreeing on the prices at which trades should occur, the current price of a stock can be interpreted as the price that takes into account all possible information. It is the price at which there are just as many informed people willing to bet that the price will go up as are willing to bet that the price will go down. In other words, at any moment, the current price is the price at which all available information suggests that the probability of the stock ticking up and the probability of the stock ticking down are both 50%. If markets work the way Bachelier argued they must, then the random walk hypothesis isn’t crazy at all. It’s a necessary part of what makes markets run.– Quote from “The Physics of Wall Street” by James Owen Weatherall
Certainly, it wouldn’t take long until a third economist comes along and proposes yet another model. Maybe in his model humans act rational 50% of the time and randomly 50% of the time. He could argue that just like photons sometimes act like particles and sometimes as waves, humans sometimes act like as a “Homo oeconomicus” and sometimes as a “Homo randomicus” . A fitting name for his model would be the theory of the “Homo quantumicus”.
Which model is correct?
Before tackling this question it is instructive to talk about yet another example. Maybe it’s just that flying is so extremely complicated and that humans are so strange that we end up in the situation where we have multiple equally valid explanations for the same phenomenon?
The futility of microscopic theories that explain the ideal gas law
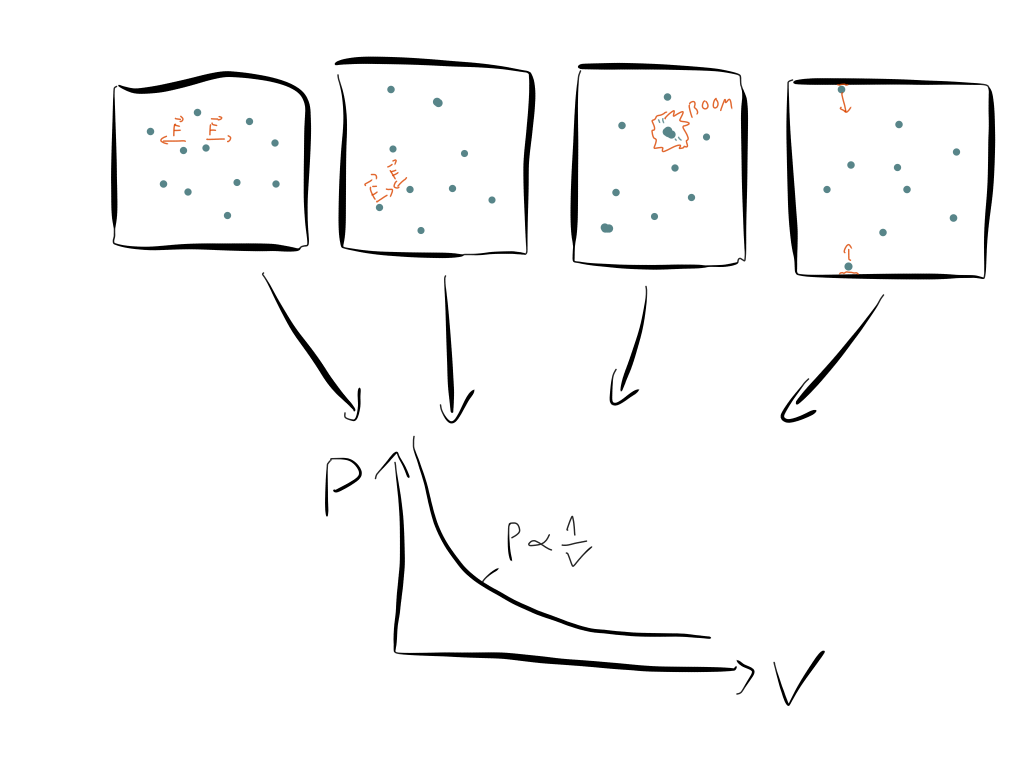
Another great example is the empirical law that the pressure of an ideal gas is inversely proportional to the volume:
$$ P \propto \frac{1}{V} $$
This means if we have a gas like air in some bottle and then make the bottle smaller, the pressure inside the bottle increases. Conversely, if we have a bottle and increase the pressure, the gas will expand the volume if possible. It’s important the relationship is exactly as written above and not something like $ P \propto \frac{1}{V^2}$ or $ P \propto \frac{1}{V^{1.3}}$. How can we explain this?
It turns out there are lots of equally valid explanation.
The first one was provided by Boyle (1660) who compared the air particles to coiled-up balls of wool or springs. These naturally resist compression and expand if they are given more space. Newton quantified this idea and proposed a repelling force between nearest neighbors whose strength is inversely proportional to the distance between them squared. He was able to show that this explains the experimental observation $ P \propto \frac{1}{V} $ nicely.
However, some time afterward he showed that the same law can be explained if we consider air as a swarm of almost free particles, which only attract each other when they come extremely close to each other. Formulated differently, he explained $ P \propto \frac{1}{V} $ by proposing an attractive short-ranged force. This is almost exactly the opposite of the explanation above, where he proposed an attractive force as an explanation.
Afterwards other famous physicists started to explain $ P \propto \frac{1}{V} $. For example, Bernoulli proposed a model where air consists of hard spheres that collide elastically all the time. Maxwell proposed a model with an inverse power law, similar to Newton’s first proposal above, but instead preferred a fifth power law instead of a second power law.
The story continues. In 1931 Lennard–Jones took the now established quantum–mechanical electrical structure of orbitals into account and proposed a seventh-power attractive law.
Science isn’t about opinions. We do experiments and test our hypothesis. That’s how we find out which hypothesis is favored over a competing one. While we can never achieve 100% certainty, it’s possible to get an extremely high quantifiable confidence into a hypothesis. So how can it be that there are multiple equally valid explanations for the same phenomenon?
Renormalization
There is a great reason why and it has to do with the following law of nature:
For laws of ideal gases this means not only that there are lots of possible explanations, but on the contrary that almost any microscopic model works. You can use an attractive force, you can use a repulsing force or even no force at all (= particles that only collide with the container walls). You can use a power law or an exponential law. It really doesn’t matter.
Your microscopic model doesn’t really matter as long as we are only interested in something macroscopic like air. If we zoom in all these microscopic models look completely different. The individual air particles will move and collide completely different. But if we zoom out and only have a look at the properties of the whole set of air particles as a gas, these microscopic details become unimportant.
The law $ P \propto \frac{1}{V} $ is not the result of some microscopic model. None of the models mentioned above is the correct one. Instead, $ P \propto \frac{1}{V} $ is a generic macroscopic expression of certain conservation laws and therefore of symmetries.
Analogously it is impossible to incorporate the individual psychology of each human into an economic theory. When we describe the behavior of large groups of people we must gloss over many details. As a result, things that we observe in economics can be explained by many equally valid “microscopic” models.
You can start with the “Homo oeconomicus”, the “Homo randomicus” or something in between. It really doesn’t matter since we always end up with the same result: stock markets move randomly. Most importantly, the pursuit of the one correct more fundamental theory is doomed to fail, since all the microscopic details get lost anyway when we zoom out.
This realization has important implications for many parts of science and especially for physics.
What makes theoretical physics difficult?
The technical term for the process of “zooming out” is renormalization. We start with a microscopic theory and zoom out by renormalizing it.
The set of transformations which describe the “zooming out” process are called the renormalization group.
Now the crux is that this renormalization group is not really a group, but a semi-group. This difference between a group and a semi-group is that there is no unique inverse element for semi-group elements. So while we can start with a microscopic theory and zoom out using the renormalization group, we can’t do the opposite. We can’t start with a macroscopic theory and zoom in to get the correct microscopic theory. In general, there are many, if not infinitely many, theories that yield exactly the same macroscopic theory.
This is what makes physics so difficult and why physics is currently in a crisis.
We have a nice model that explains the behavior of elementary particles and their interactions. This model is called the “standard model“. However, there are lots of things left unexplained by it. For example, we would like to understand what dark matter is. In addition, we would like to understand why the standard model is the way it is. Why aren’t the fundamental interactions described by different equations?
Unfortunately, there are infinitely many microscopic models that yield the standard model as a “macroscopic” theory, i.e. when we zoom out. There are infinitely many ways to add one or several new particles to the standard model which explain dark matter, but become invisible at present-day colliders like the LHC. There are infinitely many Grand Unified Theories, that explain why the interactions are the way they are.
We simply can’t decide which one is correct without help from experiments.
The futility of arguing over fundamental models
Every time we try to explain something in terms of more fundamental building block, we must be prepared that there are many equally valid models and ideas.
The moral of the whole story is that explanations in terms of a more fundamental model are often not really important. It makes no sense to argue about competing models if you can’t differentiate between them when you zoom out. Instead, we should focus on the universal features that survive the “zooming out” procedure. For each scale (think: planets, humans, atoms, quarks, …) there is a perfect theory that describes what we observe. However, there is no unique more fundamental theory that explains this theory. While we can perform experiments to check which of the many fundamental theories is more likely to be correct, this doesn’t help us that much with our more macroscopic theory which remains valid. For example, a perfect theory of human behavior will not give us a perfect theory of economics. Analogously, the standard model will remain valid, even when the correct theory of quantum gravity will be found.
The search for the one correct fundamental model can turn into a disappointing endeavor, not only in physics but everywhere and it often doesn’t make sense to argue about more fundamental models that explain what we observe.
PS: An awesome book to learn more about renormalization is “The Devil in the Details” by Robert Batterman. A great and free course to learn more it in a broader context (computer science, sociology, etc.) is “Introduction to Renormalization” by Simon DeDeo.
This is a great article. I am really inspired and feel liberated by it in some way. Many times I felt uncomfortable about many explanations in the humanities and in the soft sciences which look rational and sensible, yet, I thought it was possible to present different explanations, but uncomfortably accepted what has been given to me because it is accepted by the experts in the field. With your Boyle’ law example (I have never known of all those different attempts at microscopic explanations) you have shown me how I can take many of the unverified explanations with an open mind.
We need to distinguish between two sets of explanations; first, macroscopic phenomena explained in terms of macroscopic concepts such as the flight of airplanes and second, macroscopic phenomena explained in terms of microscopic concepts such as Boyle’s law in terms of the laws governing the gas molecules.
For the first kind of explanations, we need to distinguish between the phenomenon such as the boiling of a liquid and the process which leads to the phenomenon. For example, the same phenomenon or effect can be produced by two different processes such as one can boil a liquid by raising its temperature while keeping the pressure constant or by decreasing the pressure and keeping the temperature constant or by both means simultaneously.
It is also possible to explain the same phenomenon and process in different equivalent ways such as a body sliding down a frictionless inclined plane. It can be looked at in terms of the effect of forces on the body or the conservation of mechanical energy.
In the article, the flight of airplanes is explained as being caused by two different processes, namely by thrust or by Bernoulli’s principle. Now the two are not equivalent mechanically. But we must have one right explanation for a process, otherwise we will not have one true classical mechanics or one true model, namely Newton’s laws of motion. I believe that the two processes are simultaneously participating in the phenomenon of the flight of an airplane (as in the example of boiling a liquid above) with each contributing differently at different stages of the flight. My conjecture is that thrust would contribute more at the take off and less when the plane is flying smoothly in a straight line.
Finally, in my opinion, it remains a useful endeavour to try and guess the kind of microscopic behaviour that leads to macroscopic behaviour even if many possible microscopic behaviours lead to the same results because, 1- may be at intermediate scales or at certain critical conditions, the various models would predict different behaviours, 2- the process also encourages research in the fine structure of the system for distinguishing between the explanations, and 3- the exercise is also good for training students. There could also be more good reasons.
Notes:
1. the sentence “Conversely, if we have a bottle and increase the pressure, the gas will expand the volume if possible” may be confusing for the non-physicist by giving the impression that the volume of a gas will increase if the pressure is increased.
2. The only model Maxwell proposed for the ideal gas, as far as I know, was freely moving particles colliding elastically with the walls of a container. Was his model of an inverse power law, with the fifth power of the distance between two particles, one of his first attempts at explaining Boyle’s law?