Origin of the term Delta FUNCTION

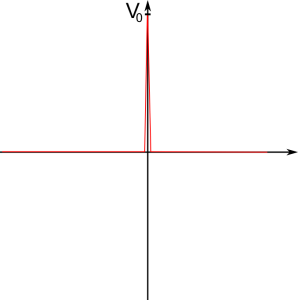
In a theoretical physics exam, we had to solve the problem to draw the potential given be $V(x)= \delta(x) V_0$. The “correct” solution can be seen in this picture. A fellow student drew the potential up to infinity, which resulted in zero points. Uhhm… Sir? Even long discussions afterwards did not change the correctors mind.

Mathematicians get, at least, goosebumps if you say it. Most physicists are aware of the fact that it is somehow incorrect to say. Nevertheless, the word is so common among physicists: Delta function.

The object that extracts the value of a function at parameter value zero

$ \tilde \delta(f(x)) = f(0)$

is not a function, but a distribution. In this short posts I want to explore a bit the connection between the two notions: delta distribution and delta function (which makes some sense after all).

Let’s start with the correct, modern, abstract definition of a distribution, as a special kind of one-form:

The distributions are the dual space of one forms to the vector space of all $C ^\infty$ (=infinitely differentiable) real-valued functions defined on the interval $-1 <= x <=1$ of $R^1$. This vector space is commonly denoted $C[-1,1]$.

(It is a group under addition (the sum of two $C ^\infty$ function is again $C ^\infty$ etc.)  and a vector space under the multiplication by real constants.)

Phew… maybe some things need explanation:

The vectors of this vector space are functions. One may confuse not this usage the word vector with the arrow-type vectors. In modern mathematics, anything that behaves like the arrow-type vectors (addition, multiplication with constants etc.) is called vector. This can be quite confusing, but one has to get used to the fact that the word vector isn’t used exclusively for arrows in euclidean space.

A one-form is an object $\tilde w()$ that eats a vector $V$ and spits out a number $\tilde w(V)$, in the same sense a function eats a number $x$ and spits out another number $f(x)$. The one-forms are called the dual object to vectors, because we can think of a vector as an object $V$ that eats a one-form $\tilde w()$ and spits out a number: $\tilde w(V)$.

The delta distribution $\tilde \delta()$ eats a vector (= a function living in $C[-1,1]$as explained above), $f(x)$ and spits out a number $\tilde \delta( f(x))=f(0)$: The function value at parameter value zero.

This is how mathematicians think about the delta thing.

Historically, the delta object was introduced by Dirac, who defined the delta thing by its property $\tilde \delta( f(x))=f(0)$. Physicist were the first to use the delta thing and the theory of distributions came afterwards.

Lacking a better word, the delta thing was called delta function. Of course, there is no function, in any mathematical precise sense, with the property $\tilde \delta( f(x))=f(0)$, but we can make some sense of the notion delta function.

The idea is that it is possible to transform any vector (here a function) $g(x)$ in $C[-1,1]$ into a one form. The one-form $\tilde g()$ could, for example, spit out, for an arbitrary function $f(x)$, the number

\begin{equation} \tilde g( f(x)) =  \int_{-1}^1 g(x)f(x) dx.
\end{equation}

The idea behind the delta function is to turn this idea around. Given a one form $  \tilde \delta()$, we can talk about a delta function $\delta(x)$ as the object that gives  the function value at parameter value zero, when integrated together with $f(x)$:

\begin{equation}   \tilde \delta(f(x))=\int_{-1}^1 \delta(x)f(x) dx = f(0)
\end{equation}

This delta “function” idea does not blow up as long as it stays under the integral. Nevertheless, there is no function $R^1 \rightarrow R^1$ (map from a number to a number), in any mathematical precise sense, with this property. Physicists treated   $\delta(x)$ like a normal function and differentiated and integrated it. Again, this only makes sense as long as we are talking of  $\delta(x)$ in combination with an integral:

\begin{equation}  \int_{-1}^1 \delta'(x) f(x) dx = –  \int_{-1}^1  \delta(x) f'(x) dx= – f'(0) , \end{equation}
where we integrated by parts.