What an imperfect world it would be if every symmetry was perfect
B. G. Wybourne
Symmetry breaking is an incredibly important phenomenon in modern physics. The best theory of nature at the fundamental level that we have, the standard model, wouldn’t make sense without it. Mathematically, symmetry breaking is easy to describe.
What is much harder is to understand intuitively what is going on.
For example, every advanced student of physics knows Goldstone’s theorem. The punchline of the theorem is that every time a symmetry gets broken, massless particles automatically appear in the theory. These particles are known as Goldstone bosons.
So far, so good.
However, what almost no student knows is why this happens. In addition to the punchline, the only thing that is presented in the standard textbooks and lectures is a proof of the theorem. But knowing the punchline + knowing that you can somehow prove the punchline does not equal understanding. To express it in terms I introduced here: what is missing is a “first layer” explanation. Students are usually only shown abstract second and third layer explanations.
I strongly believe there is always an intuitive explanation and at least Goldstone’s theorem and the famous Higgs loophole are no exceptions.
Symmetry Breaking Intuitively
Speaking colloquially, a symmetry is broken when the system we are considering is in some sense stiff. Before we consider a stiff system and why this means that a symmetry is broken, let’s consider the opposite situation first.
A gas of molecules is certainly not stiff. Consequently, we have the usual symmetries: rotational symmetry and translation symmetry.
What this means is the following:
The molecules move chaotically and if you close your eyes for a moment, I perform a global translation, i.e. move all molecules in some direction, you open your eyes again, it is impossible for you to tell that I changed something at all. The is the definition of a symmetry: You close your eyes, then I perform a transformation on an object/system and if you can’t tell that I changed anything at all, the transformation I performed is a symmetry of the object/system.
Hence, translations are a symmetry of a gas of molecules. Equally, we can argue rotations are a symmetry of the system.
Now, systems of molecules can not only appear as a gas but also as a solid system. IF we cool down the gas it will become fluid and eventually freeze. The thing is that solid systems like an ice-crystal are stiff and possess less symmetry than a gas. This is the opposite of what most laypersons would suspect. For example, thinking about beautiful ice crystals, most people would agree immediately that ice is much more symmetric than water or steam.
However, this is wrong. An ice crystal can only be rotated by very special angles, like 120 degrees or 240 degrees and still looks the same. In contrast, water or steam can be rotated arbitrarily and always looks the same. “Looks the same” means as described above that you close your eyes, I perform a transformation, and if you can’t tell the difference, the transformation is a symmetry.
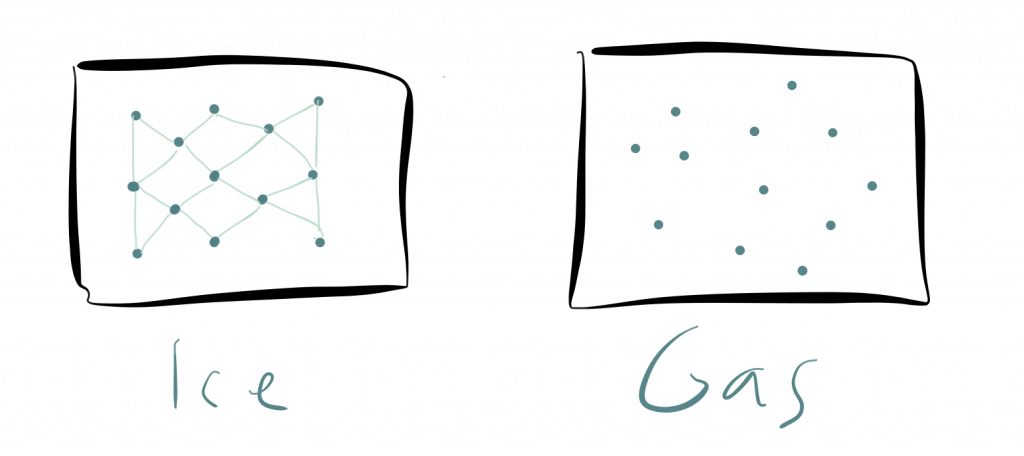
Next, we want to understand, as promised, Goldstone’s theorem intuitively. To do this, let’s first talk about energy for a moment.
A crystal consists of molecules arranged in regular, repeating rows and columns. The molecules arrange like this because the perfect arrangement in a lattice is the configuration with the lowest energy. As noted above, symmetry is broken if the atoms are arranged like this. This means directly, that I can no longer perform move the molecules around freely like I could in a gas. It now costs energy to move molecules.
With this in mind, we are ready to understand Goldstone’s theorem.
Why do we expect Goldstone bosons when a continuous symmetry gets broken?
We just noted that symmetry breaking means that a system becomes stiff. This, in turn, means that it now costs energy to move molecules around.
However, there is no resistance if we try to move all the atoms at once by the same amount. This is a result of the previously existing translational symmetry. This observation is exactly what is made precise in Goldstone’s famous theorem.
The relation between displacements and the corresponding energy cost is called dispersion relation. In technical terms, a dispersion relation describes the connection between the wavelength $\lambda$ and the frequency $\phi$ or equivalently the energy $E$. The observation mentioned above that moving all atoms at once by the same amount is a wave with infinite wavelength. The corresponding energy cost is zero because no atoms are brought closer to each other or are separated.
The interactions among the atoms are completely unaltered by such a global shift. Therefore, we have dispersion relation $\phi (\lambda) = \frac{1}{\lambda}$. As $\lambda$ goes to infinity, the frequency and thus the energy becomes zero. Such a “wave” with infinite wavelength is called in this context a Goldstone mode. While you can always consider waves with infinite wavelength in any system, the special thing here is that here they cost zero energy.
This is a result of the translational symmetry of the physical laws, which is only broken by the ground state, i.e. the perfect lattice configuration. Shifting the complete perfect lattice costs no energy. Only individual displacements cost energies. Such individual displacements correspond to waves with lower wavelength and hence have a non-zero frequency.
At a first sight Goldstone’s theorem is surprising. Why should moving all the atoms at once cost no energy, whereas small changes to the lattice structure cost much more energy?
The reason for this surprising fact is the translational invariance of the laws of physics and here of the background spacetime where we imagine our crystal lives in. The spacetime is everywhere the same and hence it makes no difference to which location we move our crystal. Hence, there is no energy penalty for changes that move the complete crystal at once.
In contrast, there is a huge energy penalty for displacing individual atoms in the lattice, because the perfect lattice is configuration with the lowest energy, In this sense, the ground state configuration is stiff.
So to summarize: Whenever we have a system that is described by physical laws which posses some symmetry, where the state with the lowest energy (the ground state) does not respect this symmetry, waves with infinite wavelength cost no energy. Expressed more concisely: Whenever a global symmetry gets broken by the ground state, we get Goldstone modes.
In a crystal low-frequency, phonons are the Goldstone modes.
Completely analogous, we can discuss what happens in a magnet. Above the Curie temperature, all the spins are aligned randomly and therefore we have rotational symmetry. However, below the Curie temperature the individual spins conspire and align in some direction. This leads to magnetic stiffness which means that the individual spins resist twists. However, a uniform twist of all spins costs not energy. The corresponding Goldstone modes are called spin waves.
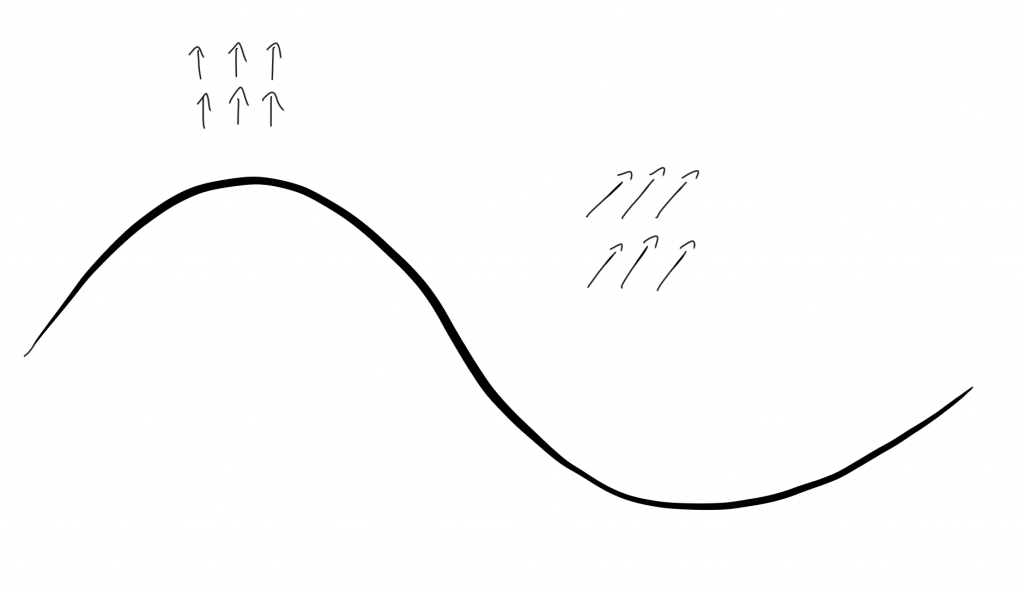
A spin wave – inspired by Fig. 8.4 in Quantum Field Theory by Lewis H. Ryder
In the ground state below the Curie temperature, all spins are aligned along some direction. This random choice of alignment breaks the rotational symmetry. The Goldstone modes correspond to those transformations that transform the various possible ground states into each other.
It is convenient to introduce the notion “order parameter” in this context. The order parameter is a way to classify in what phase a given system is in. In the case of the ferromagnet, the overall magnetization (= the total spin vector) is the order parameter.
Above the Curie temperature all spins are directly randomly and thus the total sum of all spins is zero. However, below the Curie temperature, the spins align and we get a non-zero overall spin vector = a non-zero order parameter.
A nice example to keep all this in mind is a chair. The above observation is exactly what allows us to move all the atoms in a chair at once. Instead of allowing a deformation of the lattice structure, the $10^9$ atoms that make up the chair prefer to move all at once.
In a second essay, I will try to explain which loophole Peter Higgs (and others) discovered that makes it possible to have symmetry breaking without Goldstone bosons.