Group theory is the branch of mathematics one uses to work with symmetries. A symmetry of an object is a transformation that leaves the object unchanged. The word object is chosen purposefully, because it is very vague. There is one branch of mathematics that deals with all kinds of symmetries, any kind of object can have.
The most familiar type of symmetries that come to one’s mind are symmetries of geometric shapes, so lets start with that.
Symmetries of Geometric Shapes

A square is defined mathematically as a set of points. A symmetry of the square is a transformation that maps this set of points into itself. This means concretely that by the transformation, no point is mapped to a point outside of the set that defines the square.
Obvious examples of such transformations are rotations, by $90^\circ$, $180^\circ$, $270^\circ$, and of course $0^\circ$.

A counter-example is a rotation by, say $5^\circ$. The upper-right corner point $A$ of the square is obviously mapped to a point $A’$ outside of the initial set. Of course, a square still looks like a square after a rotation by $5^\circ$, but, by definition, this is a different square, mathematically a different set of points. Hence, a rotation by $5^\circ$ is no symmetry of the square.
A characteristic property of the symmetries of the square is that the combination of two transformations that leave the square invariant, is again a symmetry. For example, combining a rotation by $90^\circ$ and $180^\circ$ is equivalent to a rotation by $270^\circ$, which is again a symmetry of the square. We will elaborate on this in the next post. In fact, the basic axioms of group theory can be derived from such an easy example.
Next, lets turn to something completely different.
Symmetries of Numbers?
Take a look at the fourth roots of unity, i.e., the (complex) numbers $z$ that give $1$ when raised to the fourth power:
\begin{equation} z^4 \stackrel{!}{=}1. \end{equation}
We can compute the solutions using the De Moivre Formula:
\begin{equation} z^n= (\cos(x)+i\sin(x))^n= \cos(nx)+i\sin(nx) \end{equation}
which follows when we write the complex number, using the Euler’s formula, as $\mathrm{e}^{ix}=\cos(x)+i\sin(x)$. The De Moivre Formula here yields,
\begin{equation} z^4= \cos(4x)+i\sin(4x) \stackrel{!}{=}1. \end{equation}
We know $\cos(2πk) + i \sin(2πk)=1$ for any integer k. The fourth roots of unity are
\begin{equation} z_k= \cos(2πk/4) + i \sin(2πk/4) \qquad \mathrm{ \ for} \qquad k = 0,1,2,3. \end{equation}
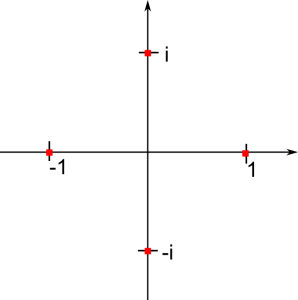
\begin{equation} \rightarrow z_0 = 1 \qquad , \qquad z_1 = i \qquad , \qquad z_2= -1 \qquad , \qquad z_3 = -i \qquad , \qquad \end{equation}
We can find a curious property of these numbers: The multiplication of two such solutions result again in a solution. Drawing the solutions in the complex plane gives us a geometric interpretation of this fact. The multiplication rotates any complex number by exactly the correct amount into another solution. The set of solutions is said to be closed under multiplication: By mere multiplication we can’t get any number that doesn’t lies in this set.
We have thus found a very similar structure in two completely different objects. On the one hand symmetries of the square, on the other hand the fourth roots of unity. Both sets contain exactly 4 objects and both share the property called closure: the combination of two objects in this set, lies again in the set. This indicates that there might be a map between the two sets, and indeed rotations in two-dimensions can be described by complex number multiplication. Exploring such intersections and structures in a systematic way is what group theory is all about.
Closure holds in general, for the n-th roots of unity, because, given two n-th roots $z,z’$, i.e. numbers for which $z^n=1$ and $z’^n=1$ holds, we have
\begin{equation} (z z’)^n = z^n z’^n = 1 \cdot 1 = 1 \quad \end{equation}
It’s no surprise that there exists a similar close relationship between the fifth-roots of unity and the symmetries of the pentagon.
We can search for higher order roots of unity and draw them in the complex plane. For example, the 100-th roots of units, i.e., the complex numbers satisfying $z^100 =1$, look like this:
These numbers are again closely related to the symmetries of a geometric object, that I don’t know the name of. Nevertheless, we can see where we are heading if we choose $n$ in $z^n=1$ to be larger and larger. Finally, we arrive at the unit circle,
The circle is quite different from the square and the pentagon, because the circle has infinitely many symmetries. Any rotation about the origin maps the circle into the circle. Such symmetries, called continuous symmetries, are the topic of a special branch of group theory, called Lie theory (after its inventor Sophus Lie).
Mathematics is a vast field. What started with integers and geometric shapes 2000 years ago, has become incredible diversified. Particular interesting things often happen at the intersection of branches of mathematics that don’t seem to have anything in common. Group theory is a framework that helps exploring such intersections.