What’s so special about the adjoint representation of a Lie group?

A representation is a map that maps each element of the set of abstract groups element to a matrix that acts on a vector space (see this post). The problem here is that at the beginning this can be quite confusing: If we can study the representation of any group on any vector space, where should we start?

Luckily, there exists exactly one distinguished representation, commonly called the adjoint representation.

First, recall some technicalities: The modern definition of a Lie group $G$ is that it’s a manifold whose elements satisfy the group axioms. Consequently, the Lie group looks in the neighborhood of any point (group element) like flat Euclidean space $R^n$ because that’s how a manifold is defined.

Now recall that the Lie algebra of a group is defined as the tangent space at the identity element $T_eG$ and Lie algebras are important, because, to quote from John Stillwell’s brilliant book Naive Lie Theory:

“The miracle of Lie theory is that a curved object, a Lie group G, can be almost completely captured by a a flat one, the Tangent space $T_eG$ of $G$ at the identity.”

I’ve written a long post about how and why this works.

It’s often a good idea to look at the Lie algebra of a group to study its properties, because working with a vector space, like $T_eG$, is in general easier than working with some curved space, like $G$. An important theoremc alled Ado’s Theorem, tells us that every Lie algebra is isomorphic to a matrix Lie algebra. This tells us that the knowledge of ordinary linear algebra is enough to study Lie algebras because every Lie algebra can be viewed as a set of matrices.

A natural idea is now to have a look at the representation of the group $G$ on the only distinguished vector space that comes automatically with each Lie group: The representation on its own tangent vector space at the identity $T_eG$, i.e. the Lie algebra of the group!

In other words, in principle, we can look at representations of a given group on any vector space. But there is exactly one distinguished vector space that comes automatically with each group: Its own Lie algebra. This representation is the adjoint representation.

In more technical terms the adjoint representation is a special map that satisfies $T(gh)=T(g)T(h)$, which is called a homomorphism, from $G$ to the space of linear operators on the tangent space at the identity $T_eG$. How does this representation look like?

A group can act on itself by left- and right-translation, given by the usual group multiplication $h \rightarrow gh$ and $h \rightarrow hg$. Both actions are not homomorphism because, denoting for example left-translation by $L_g$, i.e. $L_g(h) = gh$, we have $L_g (hj) \neq L_g(h) L_g(j)$, because $L_g(hj)=ghj \neq gh gj= L_g(h) L_g(j)$. Instead a homomorphism is given by a combination of left-translation by $g$ and right-translation by $g^{-1}$, commonly denoted by $I_g(h)=ghg^{-1}$ and called adjoint action. This is a homomorphism because

$I_g(hj)=I_g(h) I_g(j) = g h g^{-1} g j g^{-1} = g hj g^{-1} \quad \checkmark$, (using the definition of the inverse $g^{-1} g = 1$).

We have found a homomorphism that maps group elements to new group elements $I : G \rightarrow G$, but this is not a representation because $G$ is no vector space. Such a homomorphism to an arbitrary space (not necessarily a vector space) is called a realization. Nevertheless, we can use this homomorphism to derive a homomorphism to a vector space.

Firstly, take note that this homomorphism maps the identity to the identity for every group element $g$:

$I_g(e)= g e g^{-1}= g g^{-1} =e.$

If you haven’t already you should now read this post, because we will need in the following notions like curves and tangent vectors that are explained there in detail.

The property $I_g(e)=e$ means that any curve through $e$ on the manifold $G$ is mapped by this homomorphism to another (not necessarily the same) curve through $e$.Therefore the adjoint representation maps any tangent vector (of a curve on $G$) in $T_eG$ to another tangent vector in $T_eG$. In contrast left- (and right-)translations $L_g$ map tangent vectors in $T_eG$ to tangent vectors in $T_gG$.

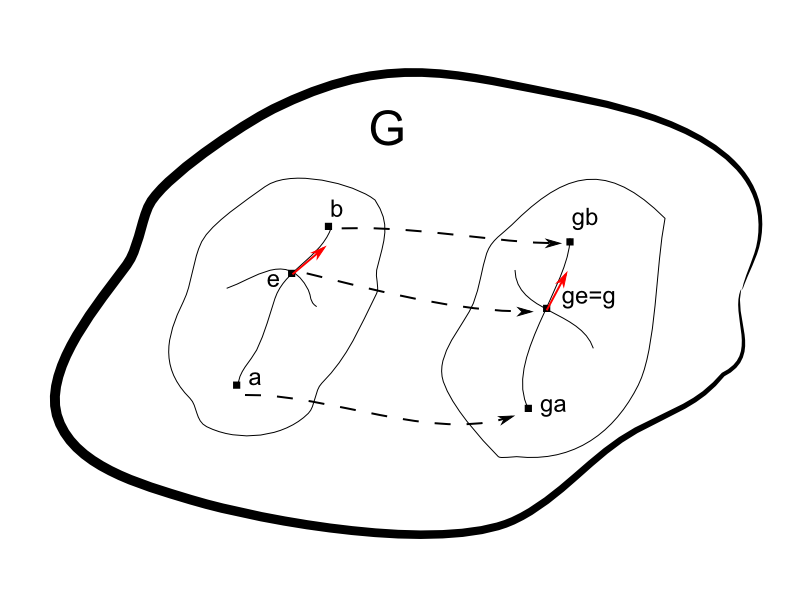
Left-translations $L_g$ map the identity $e$ to the point $g$. Therefore any curve through $e$ is mapped by $L_g$ to a curve through $g$.

The (by $I_g$) induced map of any tangent vector in $T_eG$ (an element of the Lie algebra) to another tangent vector in $T_eG$ is called the adjoint transformation of $T_eG$ induced by g. This induced map defines a representation of the group $G$ on $T_eG$, because $T_eG$ is a vector space.

In the same spirit, we can consider Lie algebra representations (in contrast to Lie group representations). Analogous this means that the elements of the Lie algebra act on some vector space as linear transformations. Again a distinguished representation is given by the action of the Lie algebra elements on the distinguished vector space $T_eG$ (the Lie algebra itself).

The corresponding homomorphism can be derived from the homomorphism that defined the representation of the group $G$ on $T_eG$. The idea goes as follows:

Consider a curve $\gamma(t)$ on the manifold $G$ with $\gamma(0)=e \in G$ and tangent vector $\gamma'(0)=X \in T_eG$. Furthermore let the curve go through some arbitrary element $g \in G$. Using this curve we can rewrite the above adjoint action

$Ad_g (X)= \underbrace{g}_{\in G} \underbrace{X}_{\in T_eG} \underbrace{g^{-1}}_{\in G}$ as $Ad_g (Y)= Ad_{\gamma(t)}(Y) = \gamma(t) Y \gamma(t)^{-1} $

We get the Lie algebra homomorphism we are searching, called $ad$ (small $a$!) by differentiating this map at the identity $t=0$. Differentiating yields

$ \frac{d}{dt} Ad_{\gamma(t)}(Y) \big |_{t=0}= \frac{d}{dt} \gamma(t) Y \gamma(t)^{-1} \big |_{t=0} = \gamma'(0) Y \gamma(0)^{-1} + \gamma(0) Y \frac{d}{dt} \gamma(t)^{-1} \big |_{t=0}$

For a matrix Lie group we can easily calculate $ \frac{d}{dt} \gamma(t)^{-1}$, because of the matrix identity

$\frac{d}{dt} A^{-1}(t)=-A^{-1}(t) \big(\frac{d}{dt} A(t)\big) \,A^{-1}(t)$.

This identity follows from

$\frac{d}{dt} \big(A(t)\,A^{-1}(t)\big)=\frac{d}{dt} \big(e \big)=0$. Using the product rule

$\big( \frac{d}{dt} A(t) \big) A^{-1}(t) + A(t) \big( \frac{d}{dt} A^{-1}(t) \big) =0$ and multiplying from the left with $A^{-1}(t)$ yields

$ \rightarrow A^{-1}(t) \big( \frac{d}{dt} A(t) \big) A^{-1}(t) = – A^{-1}(t) A(t) \big( \frac{d}{dt} A^{-1}(t) \big) = \big( \frac{d}{dt} A^{-1}(t) \big) \quad \checkmark $

Therefore we have

$ \frac{d}{dt} Ad_{\gamma(t)}(Y) \big |_{t=0}= \frac{d}{dt} \gamma(t) Y \gamma(t)^{-1} \big |_{t=0} $

$= \gamma'(0) Y \gamma(0)^{-1} + \gamma(0) Y (-\gamma(0)^{-1} \gamma'(0) \gamma(0)^{-1}) = XY e – e Y eX e $

$ = XY-YX$, where we used the definitions for the curve we made above ($\gamma(0)=\gamma(0)^{-1}=e$ and $\gamma'(0)=X)$.

We see that the adjoint action of the Lie algebra on itself is given by commutator. Thus, this is a way of seeing that the Lie bracket is the natural product of the tangent space $T_eG$, i.e. of the Lie algebra. The representation of the Lie algebra on itself is given by the adjoint action $ad_X$, i.e. by the Lie bracket! (Recall that a representation is, by definition, a map.)

This a way of figure out the Lie bracket of a given group. If we aren’t considering matrix Lie groups (for which the Lie bracket is the commutator) the Lie bracket may be something different and the steps we followed above let us calculate the corresponding Lie bracket. Nevertheless, we know from Ado’s theorem that every Lie algebra can be considered as matrix Lie algebra with the commutator as Lie bracket.

In addition, the Lie algebra representation we derived above is often used as a model for all Lie algebra representations. A Lie algebra homomorphism (and therefore representation) can be defined as a map, respecting the adjoint action! To be precise:

A Lie algebra representation $(\Phi,V)$ of a Lie algebra $T_eG$ on some vector space $V$ is defined as a linear map
$\Phi$ between any Lie algebra element $X\in T_eG$ and a linear transformation $T(g)$ of some vector space $V$
satisfying $\Phi([X,Y])= [\Phi(X), \Phi(Y)]$

In the same way, a Lie group representation is defined as a linear map (to some vector space) respecting the group element combination rule $\Phi(gh)=\Phi(g)\Phi(h)$, a Lie algebra representation is a linear map (to some vector space) respecting the natural product of the Lie algebra, i.e. the Lie bracket.