Often in particle physics, we spent a lot of time speculating about what goes on at high-energies. Theories that address current problems or puzzles in particle physics, are often UV-theories (UV=ultraviolet). A UV-theory is a theory that is valid at high energy scales. For example, a popular class of UV-theories are Grand Unified Theories. In such theories, the standard model gauge group is replaced with a “better” group. This group structure would become visible at much higher energies.
This is the usual side of the energy spectrum where we expect new symmetries to show up.
While everyone expected new symmetries to show up at high energies, instead new symmetries were discovered at the other side of the energy spectrum. This other side of the spectrum is known as infrared (IR) region and corresponds to what is going at low energies.
We can always relate energy scales to length scales. A high energy scale corresponds to tiny length scales (tiny wavelengths), low energies correspond to long length scales (long wavelengths). The newly discovered symmetries are not relevant to what is going on at tiny length scales, but instead for our description of large length scales. Such symmetries are known as asymptotic symmetries.
The first discovery of a non-trivial asymptotic symmetry was a complete surprise. In 1962 Burg, Metzner and Sachs investigated the asymptotic symmetry group of general relativity. They investigated a system that becomes asymptotically flat. Imagine a large sphere in spacetime. Let’s assume all relevant stuff is inside the spacetime and thus inside the sphere spacetime is certainly curved. However, outside of the isolated system in the sphere, spacetime becomes flat, because everything that can curve spacetime is inside the sphere. Usually, to simplify the discussion, we say the sphere is infinitely large and hence that spacetime becomes flat “at infinity”. However, we do not really mean infinity. Instead what is usually meant with infinity is that it is sufficiently far away. We use the same simplification in quantum field theory. To calculate scattering amplitudes we take the integrals from $t=-\infty $ to $t=\infty$ and often integrate all over space. Analogously these infinities shouldn’t be taken literally, but simply represent, for example, a long enough time span.
Now, back to the situation investigated by Burg, Metzner, and Sachs. Inside the sphere, the relevant symmetry group is the diffeomorphism group. (The diffeomorphism group is basically the set of all transformations that do not “destroy” spacetime, i.e. do not rip holes into it etc.). In the asymptotic region where spacetime becomes flat, the naive expectation is that the relevant symmetry group is simply the symmetry group of flat spacetime, namely the Poincare group. To everyone’s surprise, this is not what Burg, Metzner, and Sachs found. They found a different symmetry group that is now called BMS group. The BMS group was the first example of a non-trivial asymptotic symmetry. In words, this discovery means that general relativity does not simply reduce to special relativity for weak fields at large distances.
Now immediately several questions pop up:
- How can we find such asymptotic symmetries?
- What about the asymptotic symmetries of the other forces like electromagnetism?
- Why should we care about them?
The answer to the third question is certainly the most important one. If you don’t care about asymptotic symmetries, there is no point in discussing how they are defined or what the asymptotic symmetry of electromagnetism is.
Why do we care about asymptotic symmetries?
I got interested in asymptotic symmetries because I wanted to understand gauge symmetries in general. The usual discussion of gauge symmetries in almost every textbook is extremely sketchy and confused me a lot. A proper discussion of asymptotic symmetries helped me immensely to understand the different types of gauge transformations (small, large, global, local). I’ll write some more about this below.
Other reasons to be interested have to do with the buzzwords: holography, memory effects, black hole information paradoxes and soft-photon theorems.
I actually know too little about these topics to write something sensible. Thus, I’ll just quote people who know more about this:
“A central motivation for these IR investigations is to understand the holographic structure of quantum gravity in 4D asymptotically flat spacetimes, which is a good approximation to the real world. This is how I came into the subject. There has been a very beautiful unfolding story over the last twenty years about the holographic structure of quantum gravity in antide Sitter space. The story begins [137] with the identification of the symmetries in anti-de Sitter space with those of its proposed holographic dual. Following this successful example, the very first question we should ask in attempting a holographic formulation of flat space quantum gravity is “What are the symmetries?”. Up until three years ago, the answer to this question was unknown. We now know [41] at the very least that the symmetry group is infinite-dimensional and includes a certain subgroup of, but not all of, the BMS group on past and future null infinity.” https://arxiv.org/pdf/1703.05448.pdf
“Although I didn’t start this IR project with black holes in mind, as usual all roads lead to black holes [40,46,156]. The IR structure has important implications for the information paradox [157]. This paradox is intertwined with the deep IR because an infinite number of soft gravitons and soft photons are produced in the process of black hole formation and evaporation. These soft particles carry information with a very low energy cost. They must be carefully tracked in order to follow the flow of information. This is hard to do without a definition of the S-matrix! Moreover, their production is highly constrained by an infinite number of exact quantum conservation laws which correlate them both with energetic hard particles and with the quantum state of the black hole itself. This requires that black holes must carry an infinite number of conserved charges, described as ‘soft hair’ in a recent collaboration with Hawking and Perry [46,156]. The information paradox cannot be clearly stated [158], let alone solved, without accounting for soft particles. The implications of soft hair are recently discussed in [126, 158–175], for example.” https://arxiv.org/pdf/1703.05448.pdf
Moreover, it was recently discovered that asymptotic symmetries, memory effects, and soft-photon theorems are actually the same thing, just viewed from different perspectives. This is an extremely surprising connection because, at a first glance, these things have nothing to do with each other.
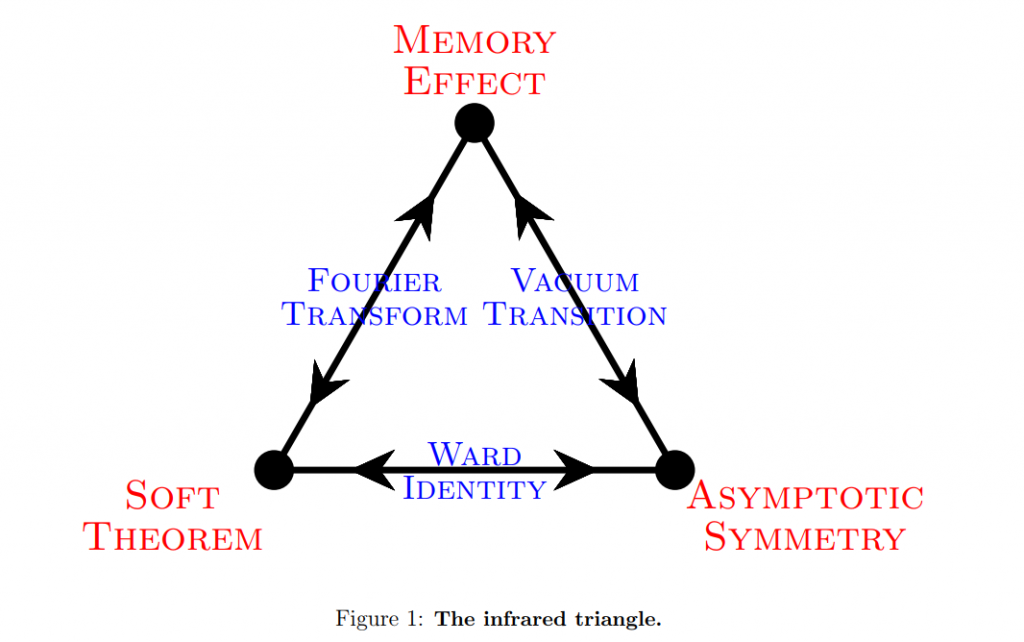
Source: https://arxiv.org/pdf/1703.05448.pdf
“Soft theorems characterize universal properties of Feynman diagrams and scattering amplitudes when a massless external particle becomes ‘soft’, i.e. its energy is taken to zero. They tell us that a surprisingly large — in fact infinite — number of soft particles are produced in any physical process, but in a highly controlled manner which is central to the consistency of quantum field theory” https://arxiv.org/pdf/1703.05448.pdf
“Soft theorems are relations between n and n + 1 particle scattering amplitudes, where the extra particle is soft. Any linear relation between scattering amplitudes can be recast as an infinitesimal symmetry of the S-matrix. It is gratifying that in some cases the resulting symmetries have turned out to be known space-time or gauge symmetries. For example Weinberg’s soft graviton theorem [20, 21] is equivalent to a symmetry of the S-matrix generated by a certain diagonal subgroup [2] of the product of BMS [22] supertranslations acting on past and future null infinity, I + and I −. This equivalence relation is of interest for several reasons. It “explains” why soft theorems exist and are so universal: they arise from a symmetry principle. Moreover, it imparts observational meaning to Minkowskian asymptotic symmetries, which have at times eluded physical interpretation. The framework has proven useful for establishing new symmetries [14] and new soft theorems [4–6]. In the quantum gravity case, the symmetries provide the starting point for any attempt at a holographic formulation, see e.g. [23]. In the gauge theory case, they are potentially useful for improving the accuracy of collider predictions, see e.g. [24].” https://arxiv.org/pdf/1407.3789.pdf
“We often think of gravitational-wave (GW) signals as having an oscillatory amplitude that starts small at early times, builds to some maximum, and then decays back to zero at late times. For example, this is the standard picture of a waveform from a coalescing compact-object binary. However, this picture is incomplete. In reality, all gravitational-wave sources possess some form of gravitational-wave memory. The GW signal from a `source with memory’ has the property that the late-time and early-time values of at least one of the GW polarizations differ from zero:
\begin{equation}
\Delta h_{+,\times}^{\rm mem} = \lim_{t\rightarrow +\infty} h_{+,\times}(t) – \lim_{t\rightarrow -\infty} h_{+,\times}(t),
\end{equation}
where $t$ is time at the observer.When a GW without memory passes through a detector, it causes oscillatory deformations but eventually returns the detector to its initial state. After a GWwith memory has passed through an idealized detector (one that is truly freely-falling), it causes a permanent deformation—leaving a `memory’ of the waves’ passage. High-frequency detectors like bars or LIGO are rather insensitive to the memory from most sources because the detector response timescale is generally much shorter than the rise-time of typical memory signals (the characteristic time for the non-oscillatory piece of the GW signal to build up to its final value). A detector like LISA is better able to detect the memory because of its good sensitivity in the low-frequency band where typical memory sources are stronger” https://arxiv.org/abs/1003.3486
“Gravitational waves are observed by geodesic deviation of nearby freely falling observers. An interesting of gravitational waves called ‘bursts with memory’ will induce permanent relative displacement of nearby observers. Such effect is the well known gravitational memory effect. […] The gravitational memory formula is nothing but the Fourier transformation of Weinberg’s formula for soft graviton production. Moreover, accompanied with an earlier discovery [8], a triangular equivalence has been found. The precise ingredients of the three corners are BMS super-translation [9], Weinberg’s soft graviton theorem and gravitational memory effect” https://arxiv.org/pdf/1703.06588.pdf
[T]he memory effect both physically manifests and directly measures the action of the asymptotic symmetries. […] The bigger picture emerging from the triangle is that deep IR physics is extremely rich, perhaps richer than previously appreciated. Every time we breathe, an infinite number of soft photons and gravitons are produced […] The gravitational memory effect imparts a physical meaning to the soft graviton theorem. Soft gravitons may seem a bit unphysical because it takes longer and longer to measure them as the energy goes to zero. Surprisingly, despite this, the memory effect can be measured in a finite time because the Fourier transform of the Weinberg pole is a step function in retarded time. In (unconfined and unhiggsed) nonabelian gauge theory, the color memory effect rotates the relative colors of nearby quarks. If a pulse of gluons passes a pair of initially singlet quarks, it will generically no longer be in a singlet. In abelian gauge theories such as QED, the electromagnetic memory effect gives relative phases to adjacent charged particles, which can be measured by quantum interference or other experiments, as recently discussed in [38, 39, 195]. […] To phrase the issue more generally, soft gravitons are produced in every scattering process. The infrared pole in the soft theorem says that their production is more ubiquitous than might have been expected. In fact, infinitely many are produced in any physical process. The soft modes are correlated with the hard modes and can store information at little or no cost in energy. Many are made in any process of black hole formation/evaporation in a manner which is highly regulated by an infinite number of conservation laws. It strikes us as implausible that we could solve the information paradox in asymptotically flat spacetime without a good understanding of these modes.
So, now that you are hopefully interested it’s time to answer the other two questions from above that I recite here for convenience: How can we find such asymptotic symmetries? What about the asymptotic symmetries of the other forces like electromagnetism?
To understand asymptotic, we first need to talk about gauge symmetries in general. There is a lot of confusion surrounding gauge symmetries and understanding them properly helps a lot. What is especially unhelpful is that almost any authors use different notions for things. So, let’s fix the meaning of the notions we use here first.
Let’s define local gauge symmetries properly
A global gauge symmetry $G = \{ g\}$ is a set of transformations that leaves the action invariant. If $G=U(1)$ a global gauge transformation is simply $e^{i a}$, with some real number $a$. In contrast, a local gauge symmetry is a set of group transformations $\mathcal{G}$ parametrized by some localized functions of spacetime. Again, for the $U(1)$ example this means that a local gauge transformation is $e^{i f(x)}$, such that $f(x) \to 0 $ for $x \to \infty$. A function $f(x)$ with this property $f(x) \to 0 $ for $x \to \infty$ is what we call a localized function. This aspect of a local gauge transformation is usually not discussed or mentioned and this is the reason for much of the confusion surrounding gauge transformations.
In words, the restriction that our local gauge transformation is parametrized by localized functions means that they only act non-trivially inside some compact bounded region. As a formula, we have: $ g(x) \to 1$ as $|x| \to \infty$ . Only such transformations truly deserve the name local gauge transformation. The global gauge group is not a subgroup of the local gauge group because global transformations do not become trivial at infinity. This is a crucial aspect that is usually overlooked. Without the restriction to localized functions, the global gauge symmetry is simply a special case of the local group with a constant function.
However, with our restriction to truly local transformations, this is no longer the case. With our definition, we can easily keep the local gauge group and the global gauge group apart. The global gauge group is responsible for the conservation laws and is a real symmetry. In contrast, the local gauge symmetry acts trivially on all observables and is merely a redundancy in our description. The local gauge group acts trivially on all physical states, whereas the global gauge group does not. The global gauge group acts non-trivially on charged states: $e^{i q}$, where $q$ is the charge.
There is one additional thing I want to mention here, although it’s not directly relevant for the following discussion. A gauge transformations can be trivial at infinity: $ g(x) \to 1$ as $|x| \to \infty$, although $f(x)$ is not zero there. This is possible, because the function $f(x)$ appears in the exponent: $e^{i f(x)}$ and the exponential function is also $1$ for $f(x) = 2 \pi$ or $f(x) = 4 \pi$ etc. The set of gauge transformations that is trivial at infinity, but where the function that parametrizes the transformation is non-zero are known as large gauge transformations. These large gauge transformations are those that carry non-zero winding number and their implications were discussed here.
What are asymptotic and global symmetries?
Now, with this in mind, we can define what asymptotic symmetries are. The asymptotic symmetry group $ASG$ for given gauge theory is defined as
$$ ASG \equiv \frac{\text{all allowed gauge symmetries}}{ \text{all gauge symmetries that are trivial at infinity } }.$$
(If you are unsure what a quotient group is, have at look at this great blog post).
Expressed differently this means the asymptotic symmetry consists of all gauge transformations that are non-trivial at infinity. As discussed above, we call gauge transformations that are trivial at infinity local gauge transformations (plus large gauge transformations), because, well, they are non-trivial only in a localized region.
Take note that this asymptotic group is not the global gauge group. The global gauge group (GGG) can be defined similarly
$$ GGG \equiv \frac{\text{all gauge symmetries that become constant at infinity}}{ \text{all gauge symmetries that are trivial at infinity} }.$$
Does this definition make sense? Elements of the global gauge group are not parametrized by spacetime coordinates. Hence they do not care about infinity and certainly do not become trivial there. However, at the same time, we must recall that elements of the global gauge group are parameterized by constant functions, i.e. numbers, and therefore cannot depend on angular variables as $|x| \to \infty$. Therefore, the global gauge transformations are given as the subset of all gauge transformations that are constant at infinity, modulo all local and large gauge transformations.
When one first encounters this definition of the global gauge group it is natural to wonder: What about they rest? What about all these transformations that are non-trivial and non-constant? Well, they are what we call asymptotic symmetries. From the definition here, we can already see that the global gauge group is a subgroup of the asymptotic symmetry group.
(Source: page 37 in Lectures on the Infrared Structure of Gravity and Gauge Theory by Andrew Strominger)
One last thing: What gets broken in the Higgs mechanism?
Finally, I want to mention one last thing that leads to far too much confusion: the spontaneous breaking of local gauge symmetries via the Higgs mechanism. It is well known that the standard story told in almost any textbook is wrong. Local gauge symmetries are 1.) not really symmetries and 2.) can’t break, which was proven by Elitzur. A proper discussion is worth its own essay, but just one short comment. A question that always pops up when people mention that spontaneous breaking of local symmetry is impossible is: “What then is the Higgs mechanism really doing?”. Well, there is symmetry breaking, but just not of the local gauge symmetry. Instead, what gets broken is the global gauge group, which we defined above as $\mathcal{G}/\mathcal{G} _* $, where
\begin{align}
\mathcal{G} _* &= \left \{ \text{ set of all } g(x) \text{ such that } g(x) \to 1 \text{ as } |x| \to \infty \right \} \\
\mathcal{G} &= \left \{ \text{ set of all } g(x) \text{ such that } g(x) \to \text{ constant element of G, not necessarily 1 as } |x| \to \infty \right \}.
\end{align}
Again, $ \mathcal{G} _*$ is the unphysical local gauge group that only represents a redundancy and acts trivially on all states and observables plus the set of all large gauge transformations). The factor group $\mathcal{G}/\mathcal{G}_* $ is the global gauge group which is responsible for the Noether charges.
(Source: Quantum Field Theory by Nair page 188 and 276)
Further reading tips:
- For some further discussion of why we care about gauge transformations that become trivial at infinity, have a look at Demystifying the QCD Vacuum: Part 2
- The best and most careful discussion of global and local gauge symmetries can be found in Symmetries, Symmetry Breaking, Gauge Symmetries by F. Strocchi.
- A nice introduction to asymptotic symmetries and their far-reaching connections is Lectures on the Infrared Structure of Gravity and Gauge Theory by Andrew Strominger. The special focus is on the many surprising connections to things like soft photon theorems. Especially interesting is the discussion in section 2.11, where he discusses that “the soft photons are the Goldstone bosons of spontaneously broken large gauge symmetry.”
- For a description of the memory effect, Electromagnetic Memory by Leonard Susskind is worth a read.
- Asymptotic symmetries of QED are discussed in New Symmetries of Massless QED by Temple He et. al.