I wrote a textbook during my master studies. People who hear about this usually ask me:
“How did this happen?”
The truth is that my book is simply a collection of things that I wrote down for myself.
Whenever I understand something, I write it down. It has happened too often to me that something doesn’t make sense to me, although I understood it a few weeks ago. Thus I’ve developed this habit of writing things down.
As my handwriting is horrible, I always write at a computer. This way I can always share quickly with others what I’ve learned. I used ShareLatex in the past, but recently switched to my own public notebook.
Most people believe that only experts should write about complicated topics. That you’re only “allowed” to write about something when you are an expert in the field.
This is a problem.
It takes a long time to become an expert. In most fields several years. During this time one easily forgets what it’s like to be a beginner. The problems one had a few months ago, now seem obvious and not worth talking about. An expert doesn’t understand the problems a beginner has because he was a beginner far too long ago.
Whenever I look back a few months I think “how stupid was I?“. The things I struggled with for weeks or even months are now obvious. When I don’t write things down, I find it impossible to recall my train of thoughts from a few months ago. In addition, most of the time I find the problems I struggled with embarrassing because their solutions are now so obvious. Thus, when I would write things down only after I’ve “mastered” the topic, I wouldn’t talk about these struggles. Either because I forgot about them or because they don’t seem important to me any longer.
However, beginners need help to overcome these hurdles. Almost everyone struggles with the same things in the beginning. Unfortunately the standard textbooks, written by experts, are here of little help. Experts find completely different things important than beginners. Most helpful are often fellow students who struggled with the same things a few days ago or if someone has written down his own learning process as a beginner. This, of course, doesn’t mean that textbooks by experts aren’t important. However, they serve a different purpose and are often not the best choice for beginners.
I’m not alone with this observation:
British writer C. S. Lewis wrote in 1958 in Reflections on the Psalms:
“It often happens that two schoolboys can solve difficulties in their work for one another better than the master can. […] The fellow-pupil can help more than the master because he knows less. The difficulty we want him to explain is one he has recently met. The expert met it so long ago he has forgotten. He sees the whole subject, by now, in a different light that he cannot conceive what is really troubling the pupil; he sees a dozen other difficulties which ought to be troubling him but aren’t.”
More recently, product designer Scott Riley tweeted:
Beginners to anything: pls document your learning shit; old fucks are bad at remembering what it was like to be new.
— Scott (@scott_riley) July 13, 2016
I think everyone should write down what they learn. Partly this already happens in the form of master and Ph.D. theses and I find these often more helpful than textbooks. However, the primary goal of a thesis is not to teach, but to present results. Therefore, one rarely reads about the struggles and things that didn’t work out.
The biggest problem here is, of course, that writing about your learnings in a form presentable to others requires time and there is almost no reward for doing this. You don’t get citations because you’re able to explain some topic better than the standard textbooks. The citations go to the authors who invented the method, not the person who can explain it beautifully. There isn’t even a good place where you can publish what you learn or beautiful explanations.
However, one possibility is to publish things on your own website. Nowadays a personal website is incredible cheap or even free. An alternative is to write a book. This requires a lot of time and the reward isn’t much bigger
I’ll continue to publish what I learn here at JakobSchwichtenberg.com. This way, I can always come back to read my own explanations for things I no longer understand and maybe someone else will find it helpful.
PS: An awesome book about the benefits of sharing more than just the final results is Show your Work by Austin Kleon.
EDIT: I recently stumbled upon the following quote “Group Theory – Birdtracks, Lie’s, and Exceptional Groups” by Predrag Cvitanovic:
Almost anybody whose research requires sustained use of group theory (and it is hard to think of a physical or mathematical problem that is wholly devoid of symmetry) writes a book about it.
and immediately was reminded of this image

Only because there are already a hundred books on a given topic, this doesn’t mean that the world doesn’t need another one. Each new writing on a given topic offers a new perspective that could be incredibly valuable for some readers.
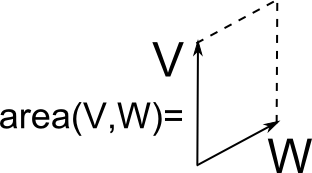
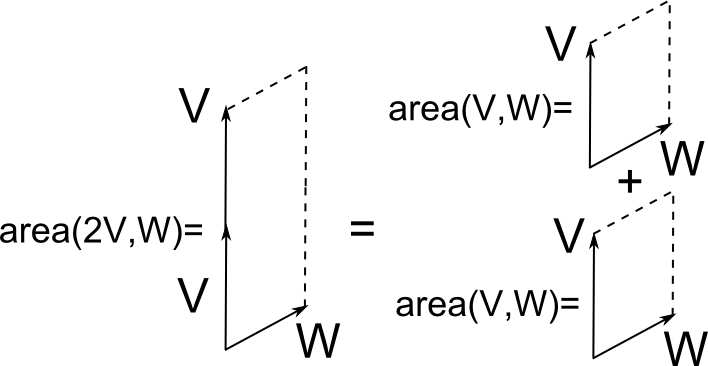
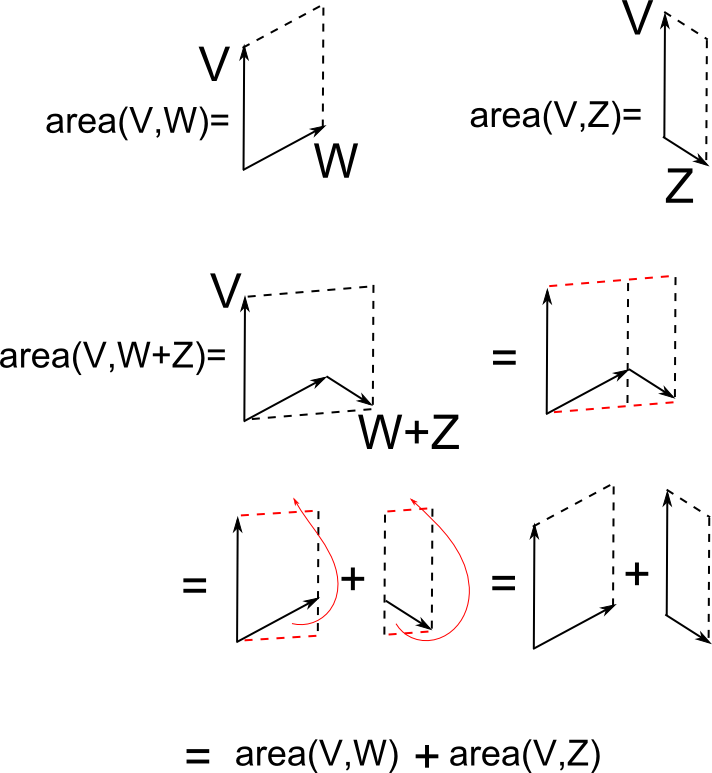
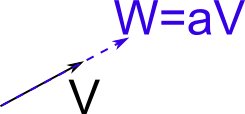 important propery is that $\mathrm{area}(V,W) $ must vanish if $V$ and $W$ are parallel, i.e. if $W=aV$ for some number $a$, we have
important propery is that $\mathrm{area}(V,W) $ must vanish if $V$ and $W$ are parallel, i.e. if $W=aV$ for some number $a$, we have