Why there is rarely only one viable explanation

“Nature is a collective idea, and, though its essence exist in each individual of the species, can never in its perfection inhabit a single object.” ―Henry Fuseli

I recently came across a WIRED story titled “There’s no one way to explain how flying works”. The author published a video in which he explained how airplanes fly. Afterward, he got attacked in the comments because he didn’t mention “Bernoulli’s principle”, which is the conventional way to explain how flying works.

Was his explanation wrong? No, as he emphasizes himself in the follow-up article mentioned above.

So is the conventional “Bernoulli’s principle” explanation wrong? Again, the answer is no.

It’s not just for flying that there are lots of absolutely equally valid ways to explain something. In fact, such a situation is more common than otherwise.

The futility of psychology in economics

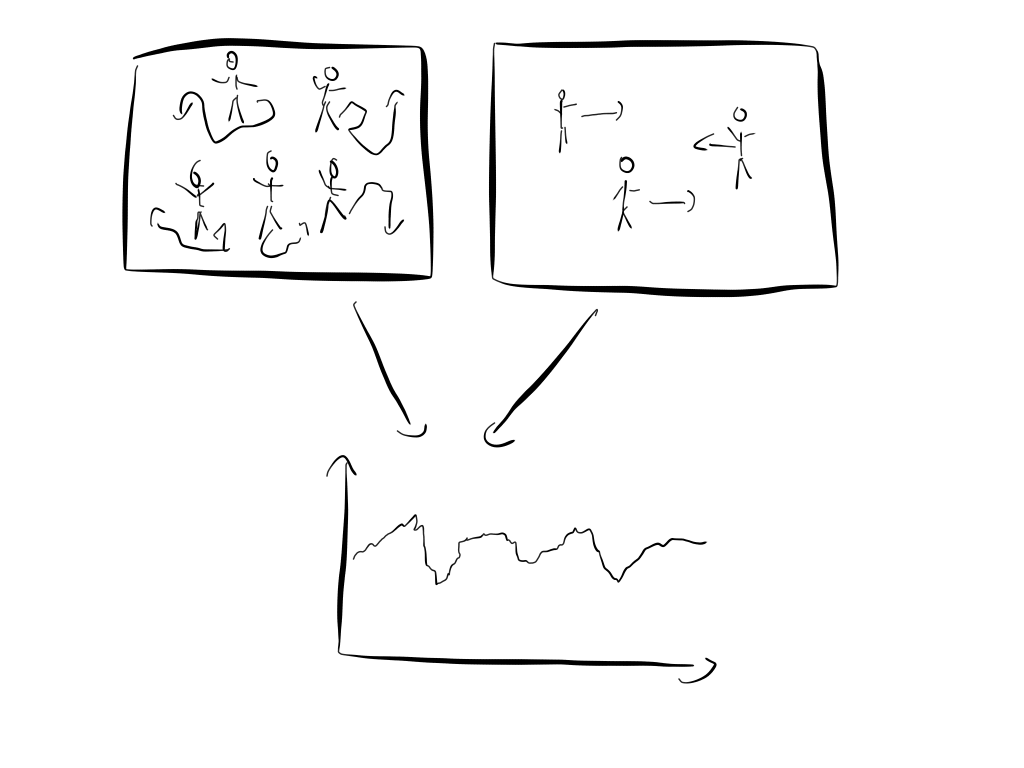
Another good example is economics. Economists try to produce theories that describe the behavior of large groups of people. In this case, the individual humans are the fundamental building blocks and a more fundamental theory would explain economic phenomena in terms of how humans act in certain situations.

An economic phenomenon that we can observe is that that stock prices move randomly most of the time. How can we explain this?

So let’s say I’m an economist and I propose a model that explains the random behavior of stock prices. My model is stunningly simple: humans are crazy and unpredictable. Everyone does what he feels is right. Some buy because they feel the price is cheap. Others buy because they think the same price is quite high. Humans act randomly and this is why stock prices are random. I call my fundamental model that explains economic phenomena in terms of individual random behavior the theory of the “Homo randomicus”.

This hypothesis certainly makes sense and we can easily test it in experiments. There are numerous experiments that exemplify how irrational humans act most of the time. A famous one is the following “loss aversion” experiment:

Participants were given \$50. Then they were asked if they would rather keep \$30 or flip a coin to decide if they can keep all \$50 or lose it all. The majority decided to avoid gambling and simply keep the \$30.

However, then the experimenters changed the setup a bit. Again the participants were given \$50, but then they were asked the participants if they would rather lose \$20 or flip a coin to decide if they can keep all \$50 or lose it all. This time the majority decided to gamble.

This behavior certainly makes no sense. The rules are exactly the same but only framed differently. The experiment, therefore, proves that humans act irrationally.

So my model makes sense and is backed up by experiments. End of the story right?

Not so fast. Shortly after my proposal another economist comes around and argues that he has a much better model. He argues that humans act perfectly rational all the time and use all the available information to make a decision. In other words that humans act as “Homo oeconomicus”. With a bit of thought it is easy to deduce from this model that stock prices move randomly.

This line of thought was first proposed by Louis Bachelier and you can read a nice excerpt that explains it from the book “The Physics of Wall Street” by James Owen Weatherall by clicking on the box below.

Why stocks move randomly even though people act rational

But why would you ever assume that markets move randomly? Prices go up on good news; they go down on bad news. there’s nothing random about it. Bachelier’s basic assumption, that the likelihood of the price ticking up at a given instant is always equal to the likelihood of its ticking down, is pure bunk. this thought was not lost on Bachelier. As someone intimately familiar with the workings of the Paris exchange, Bachelier knew just how strong an effect information could have on the prices of securities. And looking backward from any instant in time, it is easy to point to good news or bad news and use it to explain how the market moves. But Bachelier was interested in understanding the probabilities of future prices, where you don’t know what the news is going to be. Some future news might be predictable based on things that are already known. After all, gamblers are very good at setting odds on things like sports events and political elections — these can be thought of as predictions of the likelihoods of various outcomes to these chancy events. But how does this predictability factor into market behavior?

Bachelier reasoned that any predictable events would already be reflected in the current price of a stock or bond. In other words, if you had reason to think that something would happen in the future that would ultimately make a share of Microsoft worth more — say, that Microsoft would invent a new kind of computer, or would win a major lawsuit — you should be willing to pay more for that Microsoft stock now than someone who didn’t think good things would happen to Microsoft , since you have reason to expect the stock to go up. Information that makes positive future events seem likely pushes prices up now; information that makes negative future events seem likely pushes prices down now.

But if this reasoning is right, Bachelier argued, then stock prices must be random. think of what happens when a trade is executed at a given price. this is where the rubber hits the road for a market. A trade means that two people — a buyer and a seller — were able to agree on a price. Both buyer and seller have looked at the available information and have decided how much they think the stock is worth to them, but with an important caveat: the buyer, at least according to Bachelier’s logic, is buying the stock at that price because he or she thinks that in the future the price is likely to go up. the seller, meanwhile, is selling at that price because he or she thinks the price is more likely to go down. taking this argument one step further, if you have a market consisting of many informed investors who are constantly agreeing on the prices at which trades should occur, the current price of a stock can be interpreted as the price that takes into account all possible information. It is the price at which there are just as many informed people willing to bet that the price will go up as are willing to bet that the price will go down. In other words, at any moment, the current price is the price at which all available information suggests that the probability of the stock ticking up and the probability of the stock ticking down are both 50%. If markets work the way Bachelier argued they must, then the random walk hypothesis isn’t crazy at all. It’s a necessary part of what makes markets run.

– Quote from “The Physics of Wall Street” by James Owen Weatherall

Certainly, it wouldn’t take long until a third economist comes along and proposes yet another model. Maybe in his model humans act rational 50% of the time and randomly 50% of the time. He could argue that just like photons sometimes act like particles and sometimes as waves, humans sometimes act like as a “Homo oeconomicus” and sometimes as a “Homo randomicus” . A fitting name for his model would be the theory of the “Homo quantumicus”.

Which model is correct?

Before tackling this question it is instructive to talk about yet another example. Maybe it’s just that flying is so extremely complicated and that humans are so strange that we end up in the situation where we have multiple equally valid explanations for the same phenomenon?

The futility of microscopic theories that explain the ideal gas law

Another great example is the empirical law that the pressure of an ideal gas is inversely proportional to the volume:

$$ P \propto \frac{1}{V} $$

This means if we have a gas like air in some bottle and then make the bottle smaller, the pressure inside the bottle increases. Conversely, if we have a bottle and increase the pressure, the gas will expand the volume if possible. It’s important the relationship is exactly as written above and not something like $ P \propto \frac{1}{V^2}$ or $ P \propto \frac{1}{V^{1.3}}$. How can we explain this?

It turns out there are lots of equally valid explanation.

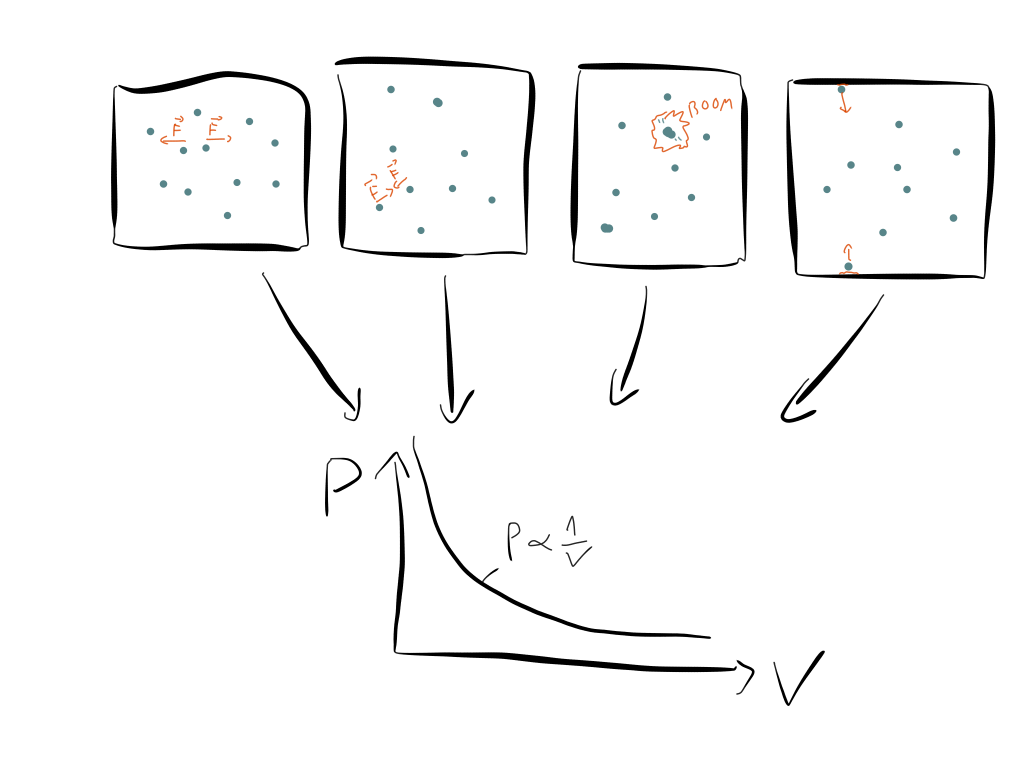
The first one was provided by Boyle (1660) who compared the air particles to coiled-up balls of wool or springs. These naturally resist compression and expand if they are given more space. Newton quantified this idea and proposed a repelling force between nearest neighbors whose strength is inversely proportional to the distance between them squared. He was able to show that this explains the experimental observation $ P \propto \frac{1}{V} $ nicely.

However, some time afterward he showed that the same law can be explained if we consider air as a swarm of almost free particles, which only attract each other when they come extremely close to each other. Formulated differently, he explained $ P \propto \frac{1}{V} $ by proposing an attractive short-ranged force. This is almost exactly the opposite of the explanation above, where he proposed an attractive force as an explanation.

Afterwards other famous physicists started to explain $ P \propto \frac{1}{V} $. For example, Bernoulli proposed a model where air consists of hard spheres that collide elastically all the time. Maxwell proposed a model with an inverse power law, similar to Newton’s first proposal above, but instead preferred a fifth power law instead of a second power law.

The story continues. In 1931 Lennard–Jones took the now established quantum–mechanical electrical structure of orbitals into account and proposed a seventh-power attractive law.

Science isn’t about opinions. We do experiments and test our hypothesis. That’s how we find out which hypothesis is favored over a competing one. While we can never achieve 100% certainty, it’s possible to get an extremely high quantifiable confidence into a hypothesis. So how can it be that there are multiple equally valid explanations for the same phenomenon?

Renormalization

There is a great reason why and it has to do with the following law of nature:

Details become less important if we zoom out and look at something from a distance.

For laws of ideal gases this means not only that there are lots of possible explanations, but on the contrary that almost any microscopic model works. You can use an attractive force, you can use a repulsing force or even no force at all (= particles that only collide with the container walls). You can use a power law or an exponential law. It really doesn’t matter.

Your microscopic model doesn’t really matter as long as we are only interested in something macroscopic like air. If we zoom in all these microscopic models look completely different. The individual air particles will move and collide completely different. But if we zoom out and only have a look at the properties of the whole set of air particles as a gas, these microscopic details become unimportant.

The law $ P \propto \frac{1}{V} $ is not the result of some microscopic model. None of the models mentioned above is the correct one. Instead, $ P \propto \frac{1}{V} $ is a generic macroscopic expression of certain conservation laws and therefore of symmetries.

Analogously it is impossible to incorporate the individual psychology of each human into an economic theory. When we describe the behavior of large groups of people we must gloss over many details. As a result, things that we observe in economics can be explained by many equally valid “microscopic” models.

You can start with the “Homo oeconomicus”, the “Homo randomicus” or something in between. It really doesn’t matter since we always end up with the same result: stock markets move randomly. Most importantly, the pursuit of the one correct more fundamental theory is doomed to fail, since all the microscopic details get lost anyway when we zoom out.

This realization has important implications for many parts of science and especially for physics.

What makes theoretical physics difficult?

The technical term for the process of “zooming out” is renormalization. We start with a microscopic theory and zoom out by renormalizing it.

The set of transformations which describe the “zooming out” process are called the renormalization group.

Now the crux is that this renormalization group is not really a group, but a semi-group. This difference between a group and a semi-group is that there is no unique inverse element for semi-group elements. So while we can start with a microscopic theory and zoom out using the renormalization group, we can’t do the opposite. We can’t start with a macroscopic theory and zoom in to get the correct microscopic theory. In general, there are many, if not infinitely many, theories that yield exactly the same macroscopic theory.

This is what makes physics so difficult and why physics is currently in a crisis.

We have a nice model that explains the behavior of elementary particles and their interactions. This model is called the “standard model“. However, there are lots of things left unexplained by it. For example, we would like to understand what dark matter is. In addition, we would like to understand why the standard model is the way it is. Why aren’t the fundamental interactions described by different equations?

Unfortunately, there are infinitely many microscopic models that yield the standard model as a “macroscopic” theory, i.e. when we zoom out. There are infinitely many ways to add one or several new particles to the standard model which explain dark matter, but become invisible at present-day colliders like the LHC. There are infinitely many Grand Unified Theories, that explain why the interactions are the way they are.

We simply can’t decide which one is correct without help from experiments.

The futility of arguing over fundamental models

Every time we try to explain something in terms of more fundamental building block, we must be prepared that there are many equally valid models and ideas.

The moral of the whole story is that explanations in terms of a more fundamental model are often not really important. It makes no sense to argue about competing models if you can’t differentiate between them when you zoom out. Instead, we should focus on the universal features that survive the “zooming out” procedure. For each scale (think: planets, humans, atoms, quarks, …) there is a perfect theory that describes what we observe. However, there is no unique more fundamental theory that explains this theory. While we can perform experiments to check which of the many fundamental theories is more likely to be correct, this doesn’t help us that much with our more macroscopic theory which remains valid. For example, a perfect theory of human behavior will not give us a perfect theory of economics. Analogously, the standard model will remain valid, even when the correct theory of quantum gravity will be found.

The search for the one correct fundamental model can turn into a disappointing endeavor, not only in physics but everywhere and it often doesn’t make sense to argue about more fundamental models that explain what we observe.

PS: An awesome book to learn more about renormalization is “The Devil in the Details” by Robert Batterman. A great and free course to learn more it in a broader context (computer science, sociology, etc.) is “Introduction to Renormalization” by Simon DeDeo.

Why experts are bad teachers* and who you should learn from instead

When I started studying it didn’t take long until I was confused and disappointed.

Why were almost all lectures boring and useless?

Typically the lecturer dwelled endlessly on trivialities and rushes with lightning speed through everything complicated. Still, I continued visiting the lectures, simply because I thought that this is how you learn at the university level. I thought somehow something will stick subconsciously even though I didn’t learn anything consciously. The main reason I went to the lectures was that I feared I would miss something crucial if I didn’t go.

I also discovered that most textbooks are boring and useless. When you go the library and read the textbook your professor recommended, you usually end up more confused. As a beginner student, you only know a few textbooks and chances are high that they are all horrible.

Today I know that I wouldn’t have missed anything if I would have skipped the lectures. Today I know that there is no way to magically learn something subconsciously. Today I know why lectures and textbooks are typically boring and useless.

What do bad lectures and textbooks have in common?

The thing that lectures and most textbooks have in common is that they are made by experts. Only after at least a decade of intensive research, you get into a position where you are allowed to give lectures. Analogously, usually, only textbooks written by experts are published or at least recommended by professors.

This sounds reasonable. To teach something you must be an expert. To write a book on something you must be an expert. What’s the problem?

The problem here is the more we know about some subject, the more we think about it in abstract terms. This isn’t a bad thing per so. Abstraction allows us to compress vast amounts of knowledge into manageable pieces. The evolution towards abstraction is the reason why every mature field has its own jargon. If you are an expert, this jargon is immensely helpful, because it allows you to express things correctly and concisely.

However, abstract explanations and jargon are big obstacles for beginners. Beginners need simple words, pictures, and analogies.

The root of all confusion

So… why aren’t experts using simple words when talking to beginners and abstract formulations when talking to fellow experts?

This question was answered in 1990 by a Stanford University graduate student in psychology named Elizabeth Newton.

She conducted an experiment in which a person was instructed to tap out a given famous song like, for example, Jingle Bells, with their fingers. A second person listened to the tapping and had to guess the name of the song.

The tappers had to estimate how many songs the person listening would guess correctly. On average they estimated that 50% of the songs would be guessed correctly. However, the real figure was only 2.5%.

The people who tapped the songs on the table heard the song in their heard and thus for them the task to guess the song seemed easy. Thus, the reason why the tapper’s estimates and the real figure are so different is that once we know something, like in the experiment the melody of the song, it’s usually incredibly hard to imagine what it’s like not knowing it.

This phenomenon is called “the curse of knowledge“. What it boils down to is that most people find it incredibly hard to put themselves in the listener’s shoes. That’s why experts talk to beginners like they would talk to a fellow expert. That’s why most textbooks and lectures are useless for their intended audience.

The curse of knowledge in the wild

Hundreds of perfect examples of the curse of knowledge in action can be seen at Scholarpedia. The project describes itself as a “peer-reviewed open-access encyclopedia, where knowledge is curated by communities of experts.” While this sounds great in theory, it’s worth examining a few articles to see how this works in practice.

Here’s an article I recently stumbled upon http://www.scholarpedia.org/article/Lagrangian_formalism_for_fields.

I was astonished how useless and confusing it is for any beginner. The problems start right at the beginning. The introductory sentences are incredibly overstuffed with buzzwords and jargon. Then in the first section, instead of sticking to the 4-dimensional spacetime we are living in, the article “explains” everything for a general D–dimensional space-time. This is something only experts care about and that can confuse beginners immensely. Finally, check out the references. There is not one article or book among them that I would recommend to a beginner student. Every beginner will be hopelessly confused after reading this article.

So without any doubt, the author of the Scholarpedia article knows what he is writing about. But unfortunately, he is subject to the curse of knowledge.

Another good place to observe the “curse of knowledge” in action is Wikipedia.
Almost any page on a math topic is completely useless for a beginner. The reason for this is, of course, that nowadays almost any math page was (re-)written by an expert. On the one hand, this is a good thing, because it means that most things on Wikipedia are nowadays correct. Wikipedia has reached a high-level of accuracy. Nevertheless, this also makes Wikipedia a horrible place to learn things. Unfortunately, most experts are not only subject to the curse of knowledge but also think that explanations in simple terms are a bit silly, trivial and naive. Thus when you try to add some explanations to Wikipedia that would be valuable for beginners, they almost always get deleted immediately.

Wikipedia wants to offer one page on a given topic that caters to all audiences. However, what experts find illuminating can confuse a beginner endlessly. There is no way to present a topic such that is a great read for any audience.

Okay fine, this is a problem. But what’s the solution?

I quote it all the time, but here it is once more:

“It often happens that two schoolboys can solve difficulties in their work for one another better than the master can. […] The fellow-pupil can help more than the master because he knows less. The difficulty we want him to explain is one he has recently met. The expert met it so long ago he has forgotten. He sees the whole subject, by now, in a different light that he cannot conceive what is really troubling the pupil; he sees a dozen other difficulties which ought to be troubling him but aren’t.” (C. S. Lewis)

The only possibility to fight the curse of knowledge is to write down what you learn while you learn it. This way you can always see what problems you struggled with when you were a beginner. After this realization, I started to write down everything I learn and I encourage others to do the same.

Unfortunately, many beginners feel that their notes are not valuable and their thoughts aren’t good enough to be written down. Nothing could be further from the truth. Only because there are already 50 textbooks on a topic by experts, this doesn’t mean that notes written by a beginner can’t help hundreds of fellow students.

For example, before I wrote my book “Physics from Symmetry” already hundreds (!) of textbooks on group theory and symmetries in physics existed. To quote Predrag Cvitanovic

“Almost anybody whose research requires sustained use of group
theory (and it is hard to think of a physical or mathematical problem
that is wholly devoid of symmetry) writes a book about it.”

Nevertheless, after my book was published I received dozens of messages from students all around the world who told me my book was exactly what they needed. This is not some lame attempt to brag. Instead, I mention this to demonstrate that what beginner writes can be valuable for others, especially fellow students.

Of course, not everyone has the time to write a complete book. For this reason, I started a small project called the Physics Travel Guide.

It’s also a wiki like Wikipedia and Scholarpedia, but it contains multiple layers. This means that it takes the various layers of understanding into account by offering several versions of each page.

Each page contains a laymen section that explains the topic solely in terms of analogies and pictures without any equations. Then there is a student section, that uses some math but is still beginner-friendly. Finally, there is the abstract layer, called researcher section, where the topic is explained in abstract terms and as rigorous as possible.

This way everyone can find an explanation in a language he understands. In addition, people interested in participating can see what kind of information is missing and don’t get discouraged because there is already lots of high-level stuff available.

To get a better idea what I am talking about, compare the Physics Travel Guide page for the Lagrangian formalism with the Scholarpedia page I mentioned above.

PS: Even if you think such a layered Wiki is a stupid idea, please, whenever you learn something, write it down and make it publicly available. There are too few people who currently do this, although such notes are incredibly valuable for anyone who tries to learn something. It doesn’t matter if you publish what you learn on a personal blog, a personal Wiki or if you participate in a Wiki project. The only thing that matters is that we get more explanations for each layer of understanding.

*Of course, there are rare exceptions like, for example, Richard Feynman who was an expert and a great teacher.

A Superior Alternative to Rote Learning

When I was taught soccer as a kid, there was one big mantra:

repetition, repetition, repetition.

We learned to pass by standing in front of each other and passing the ball between us for 20 minutes. We did this almost every training session. The same way we learned headers. We learned shooting by shooting onto the goal for half an hour at the end of every training session.

It wasn’t fun, but it worked. After several years of weekly practice, I’m quite good at soccer.

When I was a bit older I learned to play trumpet and the mantra was again:

repetition, repetition, repetition.

I had to repeat certain songs until I was able to play them perfectly. I’m sure this method would have worked again if I hadn’t given up after 2 years or so.

The same teaching method was used to teach me mathematics, Latin etc. in school. I learned to solve equations by solving hundreds of them. I learned to integrate by integrating hundreds of integrals. I learned Latin vocabularies by repeating them over and over again.

The story continued when I learned physics at university. To pass exams I had to know the exercise sheets by heart. Thus I calculated them over and over again until I had memorized every step.

Again it wasn’t fun but worked. Rote learning is certainly a valid approach, but is it really the best we can do?

It turns out, there is another teaching method that is not only much more fun but also far more effective. It’s called differential learning. Currently, this approach is only somewhat widespread in sports, but I’m convinced that it’s applicable almost everywhere.

Introducing: Differential Learning

The basic idea is this:

Instead of letting someone repeat the correct way to do something over and over again, you actively him/her them to do it wrong.

For instance, if I want to teach soccer to kids, I don’t let them repeat the correct passing technique over and over again. Instead, I tell them to pass the ball in every correct and incorrect way possible.

A good way to pass a ball is to use inside of the foot. I let them do this, but also tell them to do it in every other way possible. They have to use the outer part of their foot. They have to use the back of their foot. They have to use the bottom of their foot. They even have to pass the ball with their shin.

This way they learn to control the ball and pass it cleanly much quicker. They are immediately exposed to the differences between correct and inferior techniques. That’s why it’s called differential learning. The kids learn to adapt and find their own style. Most importantly, the brain doesn’t get bored and keeps learning and learning.

This method is surprisingly new. It was first put forward in 1999 by the German sports scientist Wolfgang Schöllhorn. However, it became popular quickly, at least in the soccer world. For example, the former coach of Borussia Dortmund, Thomas Tuchel, used it with great success. In addition to such anecdotal evidence there is serious research going on and so far, the data looks convincing.

So ist differential learning limited to sports?

Absolutely not. It’s easy to imagine how the same basic idea could be applied in other fields. However, I don’t know any examples where differential learning is currently used outside of the soccer world. This means we need to get creative.

My field is physics, so I will use it as an example. Let’s say we want to teach quantum mechanics.

The thing is if you pick up any textbook on quantum mechanics, all you find is the standard story, repeated over and over again. I recently helped a friend who was preparing for her final exam and was shocked when I saw again how similar all the textbooks are. What you’ll never find in these textbooks is disagreement or discussions of alternatives. However, this would be exactly what we need to make differential learning of quantum mechanics possible.

So how could differential learning of quantum mechanics look like in practice?

First, let’s remind ourselves how differential learning of soccer works. Afterward, we can try to map the essential steps to quantum mechanics. To teach kids soccer, we need to identify the fundamentals: passing, shooting, headers, tackles, stopping, etc. Then we let them execute these fundamentals, but make sure that they do it in every wrong and right way possible. The goal is that the kids learn to control the ball in all kinds of situations and are able to move the ball wherever they want it to be on the pitch.

So what are the fundamentals of quantum mechanics and what do we want our students to be able to do? Our goal is that students are able to describe the behavior of elementary particles in all kinds of situations:

when they are alone and moving freely,
when they are confined in a box,
when they are bound to another particle,
when they scatter off a wall,
when they are shot onto a wall with slits in it,
when they move in a magnetic field etc.

The differential way to teach this would be to give the students the task to describe particles in these situations, together with the experimental data that tells them what actually happens. We don’t force the correct way to do it onto them. Instead, we encourage them to try it in every wrong way possible.

This way we can avoid that the students simply memorize the usual quantum algorithm* without understanding anything.

This is exactly what goes wrong in the standard approach. Like the kids learning soccer by repeating the “correct way” to do something over and over again, students of quantum mechanics usually only learn to apply the standard quantum algorithm again and again.

Instead, through differential learning, they would not only be able to describe what the particles do in all these situations but actually, understand why the description works.

That’s just one example, but it’s easy to apply the principles of “differential learning” to any other topic. I would love to see people implement it in all kinds of fields. So, if you know any existing course that makes use of “differential learning” or has any ideas of how and where it could be used, please let me know.

*The algorithm is so simple that it is easily possible to apply it without any deeper understanding: Write down the Hamiltonian for the system in question, put it into the Schrödinger equation, solve it and while doing so take care of the boundary conditions. The solution is a function of space $x$ and the square of the absolute value of the solution gives you the correct probability to find the particle at any place you want to know about. You can simply memorize it, together with the Schrödinger equation and you’ll be able to solve almost any problem your professor throws at you in an exam.

PS: There are, of course, still lots of details missing in the alternative quantum mechanics course outlined above. However, it’s on my to-do list for next year to fill in the gaps and develop a fully-fledged quantum mechanics mini-course that applies the principles of “differential learning”.