Update: I’ve now started a website motivated by the idea outlined in this post. It’s called Physics Travel Guide.com. For each topic, there are different layers such that everyone can find an explanation that speaks a language he/she understands.
Over the years I’ve had many discussions with fellow students about the question: when do you understand something?
Usually, I’ve taken the strong position that is summarized by this famous Vonnegut quote:
“any scientist who couldn’t explain to an eight-year-old what he was doing was a charlatan.”
In other words: you’ve only understood a given topic if you can explain it in simple terms.
Many disagree. Especially one friend who, studies math, liked to argue that some topics are simply too abstract and such “low-level” explanations may not be possible.
Of course, the quote is a bit exaggerated. Nevertheless, I think as a researcher you should be able to explain what you do to an interested beginner student.
I don’t think that any topic is too abstract for this. When no “low-level” explanation is available so far, this does not mean that it doesn’t exist, but merely that it hasn’t been found yet.
In my first year as a student, I went on a camping trip to Norway. At that time, I knew little math and nothing about number theory or the Riemann zeta function. During the trip, I devoured “The Music of the Primes” by Marcus Du Sautoy. Sautoy managed to explain to a clueless beginner student why people care about prime numbers (they are like the atoms of numbers), why people find the Riemann zeta function interesting (there is a relationship between the complex zeros of the Riemann zeta function and the prime numbers) and what the Riemann hypothesis is all about. Of course, after reading the book I still didn’t know anything substantial about number theory or the Riemann zeta function. However, the book gave me a valuable understanding of how people who work on these subjects think. In addition, after several years I still understand why people get excited when someone proposes something new about the Riemann hypothesis.
I don’t know any topic more abstract than number theory and if it is possible to explain something as abstract as the Riemann zeta function to a beginner student, it can be done for any topic, too.
My point is not that oversimplified PopSci explanations are what all scientists should do and think about. Instead, my point is that any topic can be explained in non-abstract terms.
Well maybe, but why should we care? An abstract explanation is certainly the most rigorous and error-free way to introduce the topic. It truly represents the state of the art and how experts think about the topic.
While this may be true, I don’t think that this is where real understanding comes from.
Maybe you are able to follow some “explanation” that involves many abstract arguments or some abstract proof and maybe afterward you realize that the concept or theorem is correct. However, what is still missing is some understanding of why it is correct.
Here is a great example, from the book “Street-Fighting Mathematics” by Sanjoy Mahajan:
There is a formula that tells you the result for the sum of the first $n$ odd numbers:
$$ S_n = 1+ 3 +5 + \ldots + (2n-1) = \sum_1^n (2k-1) = n^2$$
You can proof this, for example, by induction. After such a proof you are certainly convinced that the formula $\sum_1^n (2k-1) = n^2$ is correct. But still, you have no idea why it is correct.
Now, instead consider the following pictorial explanation:
We draw each odd number as an L-shaped puzzle piece:
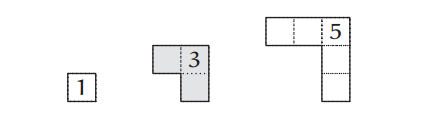
Source: Street-Fighting Mathematics by Sanjoy Mahajan
Then, we can draw the sum of the first $n$ odd numbers as follows:
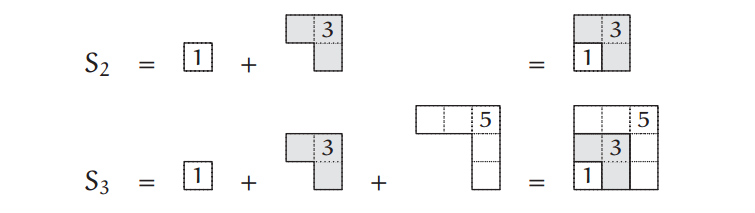
Source: Street-Fighting Mathematics by Sanjoy Mahajan
The odd numbers as puzzle pieces fit together such that we get a $n\times n$ square. We can see here that the sum is $n^2$. After seeing this proof, you’ll never forget why the sum of the first $n$ odd numbers equals $n^2$.
Especially most math books are guilty of relying solely on abstract explanations without any pictorial explanations or analogies. I personally find this oftentimes incredibly frustrating. No one gets a deep understand by reading pages full of definitions and proofs. This type of exposition discourages beginner students and simply communicates the message “well real math is complicated stuff”.
I recently read an interesting hypothesis about how this way of teaching math became the standard. In his book “Not Even Wrong” Peter Woit writes:
“What [Mathematicians] learned long ago was that to get anywhere in the long term, the field has to insist strongly on absolute clarity of the formulation of ideas and the rigorous understanding of their implications. Modern mathematics may be justly accused of sometimes taking these standards too far, to the point of fetishising them. Often, mathematical research suffers because the community is unwilling to let appear in print the vague speculative formulations that motivate some of the best new work, or the similarly vague and imprecise summaries of older work that are essential to any readable expository literature. […] The mathematics literature often suffers from being either almost unreadable or concerned ultimately with not very interesting problems […] I hope that the trend in mathematical teaching, writing, and editing will continue to recoil from the extreme of Bourbakisme, so that explanations and non-trivial examples can be presented and physicists (to say nothing of other scientists) can once more have a fighting chance of understanding what mathematicians are up to, as they did early in the twentieth century. […]’Bourbakisme’ refers to the activities of a very influential group of French mathematicians known collectively by the pseudonym Bourbaki. Bourbaki was founded by Andre Weil and others during the 1930s, partly as a project to write a series of textbooks that would provide a completely rigorous exposition of fundamental mathematical results. They felt such a series was needed in order to have a source of completely clear definitions and theorems to use as a basis for future mathematical progress. This kind of activity is what appalled Gell-Mann, and it did nothing for improving communication between mathematicians and physicists. While their books were arid and free of any examples, in their own research and private communications the mathematicians of Bourbaki were very much engaged with examples, non-rigorous argument and conjecture. […] The Bourbaki books and the point of view from which they emerged had a bad effect on mathematical exposition in general, with many people writing very hard-to-read papers in a style emulating that of the books.“
This passage reminded me of this famous quote by Chen-Ning Yang (the Yang in Yang-Mills theory):
“There are only two kinds of math books: Those you cannot read beyond the first sentence, and those you cannot read beyond the first page.”
The good news is that nowadays there exists a third kind of book that explains things pictorial and with analogies. This is where beginners should start. Here are some examples:
- Visual Complex Analysis by Tristan Needham
- Naive Lie Theory by John Stillwell
- Visual Group Theory by Nathan Carter
For example, Needham manages to give you beautiful pictures for the series expansion of the complex exponential function, which otherwise is just another formula. Another example, I’ve written about here is what is really going between a Lie algebra and a given Lie group. You can accept the relationship as some abstract voodoo or you can draw some pictures and get some deep understanding that allows you to always remember the most important results.
This problem with too abstract explanations is not only a problem in mathematics. Many physics books suffer from the same problem. A great example is how quantum field theory is usually explained by the standard textbooks (Peskin-Schröder and Co.). Most pages are full of complicated computations and comments about high-level stuff. After reading one of these books you can not help yourself but have the impression: “well, quantum field theory is complicated stuff”. In contrast, when you read “Student Friendly Quantum Field Theory” by Robert Klauber, you will come to the conclusion that quantum field theory is at its core quite easy. Klauber carefully explains things with pictures and draws lots of analogies. Thanks to this, after reading his book, I was always able to remember the most important, fundamental features of quantum field theory.
Another example from physics are anomalies. Usually they are introduced in highly complicated way, although there exists a simple pictorial way to understand anomalies. Equally, the Noether theorem is usually just proven. Students accept its correctness, but have no clue why it is correct. On the other hand, there is Feynman’s picture proof of the Noether’s theorem.
The message here is similar to what I wrote in “One Thing You Must Understand About Studying Physics“. Don’t get discouraged by explanations that are too abstract for your current level of understanding. On any topic there exists some book or article that explains it in a language that you can understand and that brings you to the next level. Finding this book or article can be long and difficult process, but it is always worth it. If there really isn’t any readable on the topic that you are interested, write it yourself!