Simple Lie groups are important, because they are in some sense the building block we can use to build up all Lie groups. Or formulated differently: simple Lie groups are the atoms of Lie theory. They are especially important in theories that unify the fundamental forces, because of the gauge group of the theory is a simple Lie group we only have one coupling constant. In contrast, the standard model gauge group $SU(3) \times SU(2) \times U(1)$ is a product of three simple groups and hence we have three different coupling constants, i.e. three different fundamental interactions.
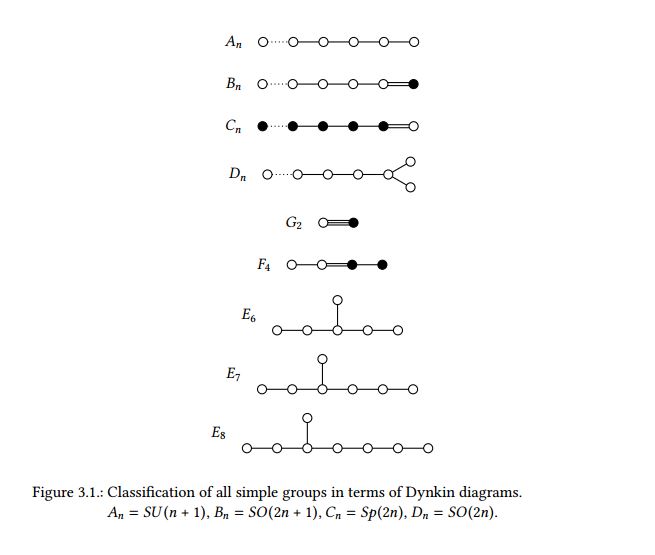
All simple Lie groups can be classified in terms of four infinite series $SU(n+1),SO(2n),SO(2n+1),Sp(2n)$ with $n\ge 1$, and five exceptional groups $G_2,F_4,E_6,E_7,E_8$.
In order to understand this classification it is instructive to use an algebraic approach to group theory. One way to define simple Lie algebras is as antihermitian matrices, which are closed under Lie bracket multiplication and fulfill the Jacobi identity
\begin{equation} \label{eq:jacobiidentity}
[[X,Y],Z]+[[Y,Z],X]+[[Z,X],Y]=0 \, .
\end{equation}
The generators of $SO(n)$ are given by antihermitian matrices with trace zero and real numbers as matrix entries. Analogously the generators of $SU(n)$ are given by antihermitian matrices with trace zero and complex numbers as matrix entries. If we now want to search for additional simple Lie groups beyond $SO(n)$ and $SU(n)$, we need to ask if there are generalized version of the complex numbers. One such generalization was found by W. Hamilton, surprisingly not with two complex units, but with three complex units $\mathrm{i},\mathrm{j}$ and $\mathrm{k}$. These four-dimensional complex numbers are called quaternions $\mathbb{H}$ and can be written as
\begin{equation}
q = a_1 + a_2 \mathrm{i} +a_3 \mathrm{j} + a_4 \mathrm{k} \,
\end{equation}
where
\begin{equation}
\mathrm{i}^2=\mathrm{j}^2=\mathrm{k}^2=-1 \text{ and } \mathrm{ijk} = -1 \quad \text{and} \quad a_1,a_2,a_3,a_4 \in \mathbb{R} \, .
\end{equation}
One curious feature of quaternions it that they do not commute $q_1 q_2 \neq q_2 q_1 $. Coming back to Lie groups, there is indeed a family of simple Lie groups given by antihermitian matrices with quaternions as matrix entries. However due to the non-commutative nature of the quaternions these generators no longer have trace zero. This family of Lie groups is known as the symplectic groups $Sp(n)$. To summarize
\begin{align}
\mathfrak{so}(n) &= \{ x \in \mathbb{R}[n]: x^\dagger = -x, \text{tr}(x)=0\} \, \notag ,\\
\mathfrak{su}(n) &= \{ x \in \mathbb{C}[n]: x^\dagger = -x, \text{tr}(x)=0\} \, \notag ,\\
\mathfrak{sp}(n) &= \{ x \in \mathbb{H}[n]: x^\dagger = -x \} \, .
\end{align}
It turns out there is exactly one additional higher-dimensional version of the complex numbers, called octonions $\mathbb{O}$, with seven complex units. These were discovered shortly after the quaternions by J. Graves. Octonions are neither commutative nor associative, i.e. $(o_1 o_2) o_3 \neq o_1 (o_2 o_3)$. Due to this curious feature, octonions can not be represented by matrices, because the matrix product is associative.
In contrast, the complex numbers, can be represented by real $2\times 2$ matrices using
\begin{equation} \label{eq:comrealmatrix} 1 \mapsto
\begin{pmatrix}
1&0 \\ 0&1
\end{pmatrix}
\qquad , \qquad
\mathrm{i} \mapsto
\begin{pmatrix}
0&-1 \\ 1&0
\end{pmatrix} \, , \notag \end{equation}
which fulfil
\begin{equation} 1^2=1, \qquad \qquad \mathrm{i}^2=-1, \qquad \qquad 1\mathrm{i}=\mathrm{i}1=\mathrm{i} .\notag \end{equation}
Analogously quaternions can be written as complex $2 \times 2$ matrices, using
\begin{equation}
\mathrm{1} \mapsto
\begin{pmatrix}
1&0 \\ 0&1
\end{pmatrix}
\quad , \quad \mathrm{i} \mapsto
\begin{pmatrix}
i&0 \\ 0&-i
\end{pmatrix} \quad , \quad \mathrm{j} \mapsto
\begin{pmatrix}
0&1 \\ -1&0
\end{pmatrix}
\quad , \quad
\mathrm{k} \mapsto
\begin{pmatrix}
0&i\\i&0
\end{pmatrix} \, \notag .
\end{equation}
In abstract terms $\mathbb{R},\mathbb{C},\mathbb{H}$ and $\mathbb{O}$ are called normed division algebras, which are defined by
\begin{align}
ab&=0 \text{ only for } a= 0 \text{ or } b=0 \, , \notag \\
N(ab)&= N(a)N(b) \, ,
\end{align}
where $a$ and be $b$ denote arbitrary elements of the algebra and $N(\cdot)$ the associated norm. It was proven by Hurwitz that the only normed division algebras are $\mathbb{R},\mathbb{C},\mathbb{H}$ and $\mathbb{O}$. For this reason normed division algebras are sometimes called Hurwitz algebras.
With this knowledge it is natural to ask if we can find, analogous to $SO(n)$ for $\mathbb{R}$, $SU(n)$ for $\mathbb{C}$ or $Sp(n)$ for $\mathbb{H}$, a family of simple Lie groups related to the octonions. Although antihermitian matrices over octonions close under the Lie bracket they do not necessarily generate Lie groups, because of the Jacobi identity (Eq. \ref{eq:jacobiidentity}). For antihermitian matrices over the reals, complexes or quaternions this requirement is automatically satisfied due to associativity. The octonions, however, are non-associative. Therefore we need more sophisticated techniques to construct Lie algebras from octonions. It turns out there are exactly five Lie algebras one can construct using octonions, called $G_2,F_4,E_6,E_7$ and $E_8$, and not infinitely many as for the reals, complexes or quaternions. The reasons is that for four of these the explicit construction the Lie algebra involves two of the normed division algebras and there are only four distinct pairs involving the octonions
- $(\mathbb{R},\mathbb{O})$ : $F_4$
- $(\mathbb{C},\mathbb{O})$ : $E_6$
- $(\mathbb{H},\mathbb{O})$ : $E_7$
- $(\mathbb{O},\mathbb{O})$ : $E_8$
Analogously one can pair all other normed division algebras, but these yield no new Lie algebras. For example, the same construction for $(\mathbb{C},\mathbb{H})$ yields $SO(12)$. The complete set of Lie algebras one gets from this construction of composition Lie algebras is usually arranged in a square, famously known as the Freudenthal magic square.
The explicit construction of these Lie algebras would lead us too far apart from the main theme of this thesis, but can be found, for example, in this paper by Pierre Ramond. The fifth exceptional group $G_2$, is the automorphism group of the octonions. This means this group is given by the set of transformations that maps the octonions onto themselves.
To summarize, all simple Lie groups can be classified because there is a close connection to normed division algebras. Hurwitz’s theorem tells us that there are only four normed division algebras $\mathbb{R},\mathbb{C},\mathbb{H}$ and $\mathbb{O}$. Each of them is closely connected to a family of simple Lie groups, $SO(n)$, $SU(n)$, $Sp(n)$ and the exceptional groups, respectively. The construction of the corresponding generators is straightforward for the infinite families $SO(n)$, $SU(n)$, $Sp(n)$, but due to the non-associative nature of the octonions quite involved for the exceptional groups. An important result is that for this reason the exceptional family has only five members $G_2,F_4,E_6,E_7$ and $E_8$.
This classification of the simple Lie groups can be nicely summarized visualized in in terms of Dynkin diagrams as shown in the following figure.