Motivation for the Group Theory Axioms

Numbers measure size, groups measure symmetry – M.A. Armstrong: Groups and Symmetry

Group theory is the mathematical tool one uses in order to work with symmetries. Because symmetries are defined as invariance under transformations, one defines a group as a collection of transformations. Let’s get started with two easy examples to get a feel for what we want to do:

1) A square is mathematically a set of points (for example, the four corner points are part of this set) and a symmetry of the square is a transformation that maps this set of points into itself.

Examples of symmetries of the square are certain (not all!) rotations about the origin. Certain rotations about the origin map the  square into itself. This means, they map every point of the set to a point that lies again in the set, and the one says, the set is invariant under such a transformation.

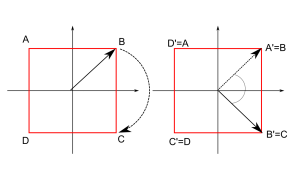
This becomes obvious if we focus on the corner points of the square. Transforming the set by a clockwise rotation by, say 5°, maps these points into points outside the original set that defines
the square. For instance, the corner point $A$ is mapped to the point $A’$, which is not found inside the set, that defined the square in the first place. Therefore a rotation by 5° is not a symmetry of the square. Of course, the rotated object is still a square, but not the same square (read: set of points). Nevertheless, a clockwise rotation by 90° is a symmetry of the square because the point $A$ is mapped to the point $B$, which lies again in the original set. Other examples of symmetry transformations of the square would be rotations by 180°, 270° and of course 0°.

Another perspective: Imagine you close your eyes for a moment, and then someone transforms the square in front of you. If you can’t tell after opening your eyes again if the other person changed anything at all, the transformation the person performed was a symmetry transformation.

The set of transformations that leave the square invariant is called a group. The transformation parameter, here the rotation angle, can’t take on arbitrary values and the group is called a discrete group.

2) Another example is the set of transformations that leave the unit circle invariant. Again, the unit circle is defined as a set of points and a symmetry transformation is a map, that maps this set into itself. 

The unit circle is invariant under all rotations about the origin, not just a few. In other words: the transformation parameter (the rotation angle) can take on arbitrary values, and the group is said to be a continuous group.

Of course, mathematics isn’t exclusively about geometric shapes and one can find symmetries of different kinds of objects, too. For instance, considering vectors, one can look at the set of transformations that leave the length of any vector unchanged. (The object that is unchanged in this case is the metric, which is the mathematical object that defines length.) For this reason, the definition of symmetry I gave at the beginning was very general: Symmetry means invariance under a transformation. Luckily, there is one mathematical tool, called group theory, that lets us work with all kinds of symmetries. (As a side note: group theory was invented historically to investigate symmetries of equations).

To make the idea of a mathematical tool that lets us deal with symmetries precise, we need to distill the defining features of symmetries in a mathematical form:

• • Leaving the object in question unchanged (“doing nothing”) is always a symmetry and therefore, every group needs to contain an identity element. In the examples above, the identity element is the rotation by 0°.

• • Transforming some object and performing afterwards the inverse transformation must be equivalent to doing nothing. Therefore, there must be, to every element in the set, an inverse element. A transformation followed by its inverse transformation is, by definition of the inverse transformation, the same as the identity transformation. In the above examplesthis means that the inverse transformation to a rotation by 90° is a rotation by -90°. A rotation by 90° followed by a rotation by -90° is the same as a rotation by 0°.

• • Performing a symmetry transformation followed by a second symmetry transformation is again a symmetry transformation. A rotation by 90° followed by a rotation by 180° is a rotation by 270°, which is a symmetry transformation, too. This property is called closure.

• • The combination of transformations must be associative. A rotation by 90° followed by a rotation by 40°, followed by a rotation by 110° is the same as a rotation by 130° followed by a rotation by 110°, which is the same as a rotation by 90° followed by a rotation by 150°. In a symbolic form: $R(110°) R(40°) R(90°)=  R(110°) \big(R(40°) R(90°)\big)= R(110°) R(130°)$  and $R(110°) R(40°) R(90°)=\big(R(110°) R(40°) \big) R(90°)= R(150°) R(90°)=$ This is called associativity. (This may not be confues with commutativity, because a the elements of a group, in general, do not commute. For example rotations around different axes: $R_x(30^\circ) R_z(40^\circ) \neq R_z(40^\circ) R_x(30^\circ) $)

• • To be able to talk about the things above one needs a rule, to be precise: a binary operation, for the combination of group elements. In the above examples, the standard approach would be to use rotation matrices and the rule for combining the group elements (the corresponding rotation matrices) would be ordinary matrix multiplication. Nevertheless there are often different ways of describing the same thing. The rotations in the plane can be described by multiplication with unit complex numbers, too. Therefore, the rule for combining group elements would be complex number multiplication. Happily, group theory lets one study such, maybe confusing, diversity in a very systematic way. This branch of group theory is called representation theory, and we will have a look at it in another post.

We are now able to see that the abstract definition of a group simply states (obvious) properties of symmetry transformations:

A group is a set $G$, together with a binary operation $\circ$ defined on $G$ that satisfies the following axioms

•  Closure: For all $g_1, g_2 \in G$, $g_1 \circ g_2 \in G$
• Identity: There exists an identity element $e \in G$ such that for all $g \in G$, $g \circ e = g = e \circ G$
• Inverses: For each $g \in G$, there exists an inverse element $g^{-1} \in G$ such that $g \circ g^{-1}=e = g^{-1} \circ $ g.
• Associativity: For all $g_1, g_2, g_3 \in G$, $g_1 \circ (g_2 \circ g_3) = (g_1 \circ g_2) \circ g_3$.