“The important thing in science is not so much to obtain new facts as to discover new ways of thinking about them.”
Sir William Lawrence Bragg
General relativity is conventionally summarized as follows:
This is the standard textbook story. Now the magic:
It also makes sense to turn the conventional “essential lesson” of General Relativity completely upside down!
When Einstein understood this, he referred to this insight as “beyond my wildest expectations.” Carlo Rovelli refers to this change of perspective as “the true magics hidden inside General Relativity“, which is where the title of this post comes from.
Now that you are hopefully interested, let’s discuss how we can achieve this change of perspective and what it means to turn the essential lesson of General Relativity upside down.
So now, let’s start. As usual in General Relativity, we need a “Gedankenexperiment” (= thought experiment).
Problems inside an empty hole
The fundamental equation of General relativity – the Einstein equation – famously stays the same under all sufficiently smooth transformations (diffeomorphisms). This means we can act with any sufficiently smooth transformation on a given solution of the Einstein equation and get another solution. The conventional name for this symmetry is “general covariance”.
While symmetries are usually great, too much of anything is harmful. The huge symmetry of General Relativity is no exception and leads to a huge problem.
We can understand the problem through the following Gedankenexperiment.
Consider a region of the universe that contains no matter – a hole. Inside this hole, we take a closer look at two specific points $A$ and $B$. At $A$ the gravitational field $e$ is flat, while at $B$ it is not.
Now, since the Einstein equation is generally covariant, we can find a transformation $\phi$ that maps $A$ to $B$ and leaves everything outside the hole unchanged. The gravitational field gets now changed to $\tilde e = \phi^\star e$. Since $A$ is mapped to $B$, the field $\tilde e$ is curved at $A$ and flat at $B$.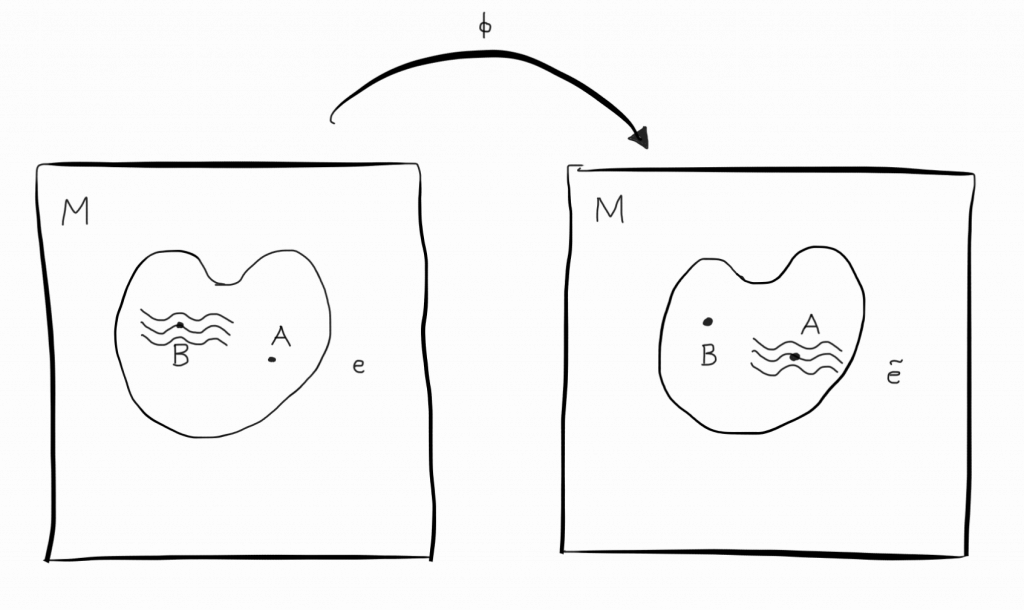
Both field configurations $e$ and $\tilde e$ are both physical solutions of the Einstein equation since our transformation $\phi$ is a symmetry.
This is a huge problem.
What is the real physics at the point $A$? Is the gravitational field flat or curved here? The Einstein equation seems to be meaningless since it doesn’t uniquely determine the gravitational field at the spacetime point $A$.
However, we know from experiments that gravity doesn’t behave strangely. We don’t need, for example, a superposition of all possible solutions. Gravitational physics is deterministic.
Now, there are only two ways out of this dilemma.
- Either we need different field equations that aren’t generally covariant and therefore determine the gravitational field at $A$ uniquely.
- Or we need to rethink the notion “spacetime point”.
Einstein actually searched for three years for non-generally covariant field equations. However nowadays, with the power of hindsight, we know that the Einstein equation is correct. Therefore, we need to talk about the second option.
What is a spacetime point?
We usually accept that there is fixed, invisible background structure that we call spacetime. We can imagine it as some kind of lattice with infinitesimal lattice spacing that permeates everything. While the actual labels that we put on this lattice do not matter, we usually accept that this invisible structure exists.

This is how we ended up with our strange conclusion in the last section that the physics at point $A$ is not uniquely determined.
However is there actually any evidence for the existence of this invisible background structure? Sure, it’s a useful tool – but as argued above it leads to problematic conclusions.
So let’s leave the invisible stuff aside and talk about things that we can actually observe.
The situation described in the last section is rather meaningless. How could we ever notice that the gravitational field is curved or flat if there is nothing except the gravitational field inside the hole?
Therefore, to probe the physics inside the hole let’s send two test particles into the hole. We further assume that these particles meet at $B$.
Now, not only the gravitational field but also the worldlines, $x_a$ and $x_b$, of the two particles are determined by the Einstein equation.
Next, we consider again the map $\phi$ from the last section.
The thing is that not only the gravitational field $e$ gets transformed, but also the worldlines $x_a$ and $x_b$! Again, $e$ becomes $\tilde e$ and in addition, $x_a$ and $x_b$ become $\tilde{x}_a$ and $\tilde{x}_b$. Since $\phi$ is a symmetry these are again physical solutions of the Einstein equation.
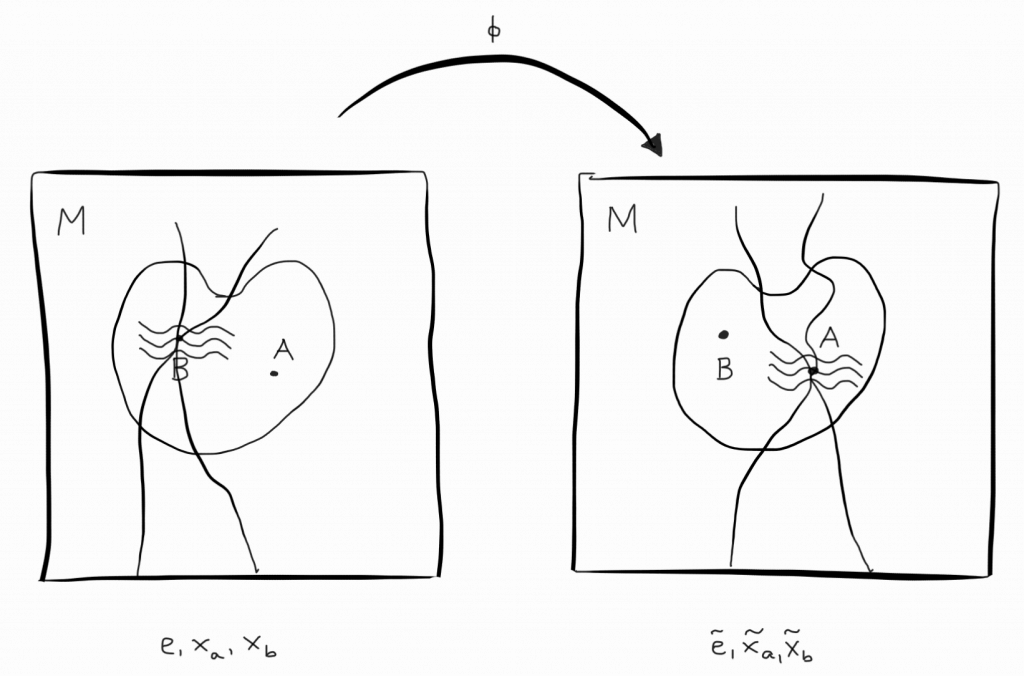
With this in mind, we can see how the paradoxical situation outlined in the last section can be resolved.
We previously asked: Is the gravitational field flat or curved at $A$?
Now, we can instead: Is the gravitational field flat or curved at the point where the two particles meet?
As discussed in the last section the first question is not uniquely answered by the Einstein equation. We can find a solution $\tilde e$ where the gravitational field is curved at $A$ and another one $e$ where it is flat at $A$.
In contrast, the second question is uniquely answered by the Einstein equation! The gravitational field is curved at the point where the two particles meet no matter what smooth transformation we apply. This is how the hole problem is solved. We were simply asking the wrong question.
The fundamental lesson of General Relativity turned upside down
What we learn through the famous “hole Gedankenexperiment” is that it makes no sense to ask questions about spacetime points. Instead, we must ask questions about locations that are determined dynamically through elements in the theory, like the two particles in the example above.
In this sense, there is no invisible background structure like we usually assume it. Instead, spacetime emerges dynamically. I like the following analogy by Rovelli
“Objects are not immersed in space. Objects make up space. Like a marriage. It’s not a man and a women feel up marriage. They are the marriage. There is no marriage without a man and a women (or a man and a man or a women and a women. Whatever.). … Space is nothing that remains if you take away all the things. Instead it’s made up by things. ”
To quote Einstein:
“All our space-time verifications invariably amount to a determination of space-time coincidences. If, for example, events consisted merely in the motion of material points, then ultimately nothing would be observable but the meeting of two or more of these points. Moreover, the results of our measurements are nothing but verifications of such meetings of the material points of our measuring instruments with other material points, coincidences between the hands of a clock and points on the clock-dial, and observed point-events happening at the same place at the same time. The introduction of a system of reference serves no other purpose than to facilitate the description of the totality of such coincidences. “
Rovelli concludes:
“The two solutions $(e,x_a,x_b)$ and $(\tilde e,\tilde {x}_a, \tilde{x}_b)$ are only distinguished by their localization on the manifold. They are different in the sense that they ascribe different properties to manifold points. However, if we demand that localization is defined only with respect to the fields and particles themselves, then there is nothing that distinguishes the two solutions physically. […] It follows that localization on the manifold has no physical meaning. […] Reality is not made by particles and field on a spacetime: it is made by particles and fields (including the gravitational field), that can only be localized with respect to one another. No more fields on spacetime: just field on fields.”
While the traditional summary of General Relativity states that gravity is merely an “illusion” caused by the curvature of spacetime, the line of thought outlined above suggests instead that there is no spacetime at all!
What we perceive as spacetime emerges dynamically through interactions like gravity. In this sense, we have turned the essential lesson of General Relativity completely upside down!
There is a nice paragraph quite at the end of Rovelli’s “Quantum Gravity” book that summarizes everything said here much better than I ever could:
Einstein’s major discovery is that spacetime and the gravitational field are the same object. A common reading of this discovery is that there is no gravitational field: just a dynamical spacetime. In view of quantum theory, it is more illuminating and more useful to say that there is no spacetime, just the gravitational field. From this point of view, the gravitational field is very much a field like any other field. Einstein’s discovery is that the fictitious background spacetime introduced by Newton does not exist. Physical fields and the relations are the only components of reality.
( A short comment: the notion “dynamical spacetime” can be confusing. Spacetime is a static thing since time is already included. Hence, there is no wobbling spacetime etc. Spacetime is a fixed thing that doesn’t change.)
- Further information along these lines, can be found in the last chapter in the book Some Elementary Gauge Theory Concepts by Sheung Tsun Tsou and Hong-Mo Chan where they talk about the idea of a “pointless theory”.
- For some more philosophical thoughts, see Interpreting theories without a spacetime by De Haro and de Regt.