After being confused for several weeks about various aspects of the QCD vacuum, I now finally feel confident to write down what I understand.
The topic itself isn’t complicated. However, a big obstacle is that there are too many contradictory “explanations” out there. In addition, many steps that are far from obvious are usually treated in like two lines. I’m not going to flame against such confusing attempts to explain the QCD vacuum. Instead, I want to tell a (hopefully) consistent story that illuminates many of the otherwise highly confusing aspects.
The QCD vacuum is currently (again) a big thing. It was discussed extensively in the 80s and it is now again popular because there are lots of people working on axion physics. The axion mechanism is an attempt to explain what we know so far experimentally about the QCD vacuum. A careful analysis of the structure of the QCD vacuum implies that QCD, generally, violates CP symmetry. So far, no such violation was measured. This is a problem and the axion mechanism is one possibility to explain why this is the case.
However, before thinking about possible solutions, it makes sense to spend some time to understand the problem.
Usually, when we think about the vacuum, we don’t think that there is a lot to talk about. Instead, we have something quite boring in mind. Empty space. Quantum fields doing nothing, because they are, by definition, not excited.
However, it turns out that this naive picture is completely wrong. Especially the vacuum state of the quantum theory of strong interactions (QCD) has an incredibly rich structure and there are lots of things that are happening.
In fact, there is so much going on, that the vacuum isn’t fully understood yet. The main reason is, of course, that, so far, we always have to use approximations in quantum field theory. Usually, we use perturbation theory as the approximation method of choice, but it turns out that this is not the correct tool to describe the vacuum state of QCD.
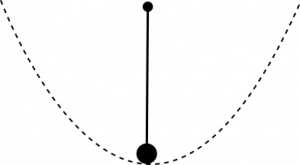
The reason for this is that there are (infinitely) many states with the minimal amount of energy, ground states, and the QCD fields can change from one ground state into another. When we study these multitudes of ground states in detail, we find that they do not lie “next to each other” (not meant in a spatial sense) but instead there are potential barriers between them. The definition of a ground state is that the fields which are in this configuration, have the minimal amount of energy and thus certainly not enough to jump across the potential barriers. Therefore, the change from one ground state into another is not a trivial process. Instead, the fields must tunnel through these potential barriers. Tunneling is a well-known process is quantum mechanics. However, it can not be described in perturbation theory. In perturbation theory, we consider small perturbations of our fields around one ground state. Thus, we never notice any effects of the other ground states that exist behind the potential barriers. We will see below how this picture of infinitely many ground states with potential barriers between them emerges in practice.
The correct tool to describe tunneling processes in quantum field theory is to use a semiclassical approximation. At a first glance, this certainly seems contradictory. There is no tunneling in a classical theory, so why should a semiclassical approximation help to describe tunneling processes in quantum field theory? The trick that is used to make the semiclassical approximation work is to substitute $t\to i \tau$, i.e. to make the time imaginary. At first, this looks completely crazy. However, there are good reasons to do this, because it is this trick that allows us to use a semiclassical approximation to describe tunneling processes. Possibly the easiest way to see why this makes sense is to recall the standard quantum mechanical problem of an electron facing a potential barrier. Before the potential barrier, we have an ordinary oscillating wave function $e^{i\omega t}$. But inside the potential barrier, we find a solution proportional to $e^{-\omega t}$. Physically, this means that the probability to find the electron inside the potential barrier decreases exponentially. By comparing the tunneling wave function with the ordinary wavefunction, we can see that the difference is precisely described by the substitution: $t\to i \tau$. In addition, we will see below that the effect of $t\to i \tau$ is basically to flip the potential upside down. Therefore, the potential barrier becomes a valley and there is a classical path across this valley. The technical term for such a tunneling process is instanton.
If this didn’t convince you, here is a different perspective: In the path integral approach to quantum mechanics, we need to sum the action for all possible paths a particle can travel between two fixed points. The same is true in quantum field theory, but there we must sum over all possible field configurations between two fixed field configurations. Usually, we cannot compute this sum exactly and must approximate it instead. One idea to approximate the sum is to find the dominant contributions. The dominant contributions to the sum come from the extremal points of the action and these extremal points correspond exactly to the classical paths. For our tunneling processes, the key observation is that there are, of course, no classical paths that describe the tunneling. Thus, without a clever idea, we don’t know how to approximate the sum. The clever idea is, as already mentioned above, to substitute $t\to i \tau$. After this substitution, we can identify the dominant contributions to the path integral sum, because now there are classical paths. At the end of our calculation, after we’ve identified the dominant contributions, we can change back again to real-time $ i \tau \to t$. This is another way to see that a semiclassical approximation can make sense in a quantum field theory.
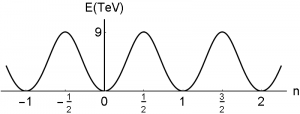
Now, after this colloquial summary, we need to fill in the gaps and show how all this actually works in practice. We start by discussing how the QCD vacuum picture with infinitely many ground states, separated by potential barriers, comes about. Afterward, we discuss how there can be tunneling between these ground states and then we write down the actual ground state of the theory. This real ground state is a superposition of the infinite number of ground states. The final picture of the QCD vacuum state will be completely analogous to the wave function of an electron in a periodic potential. In nature, such a situation is realized, for example, in a semiconductor. The electron does not sit at one of the many minimums, but is instead in a state of superposition, because it can tunnel from one minimum of the potential to another. The correct wave function for the electron in this situation is known as a Bloch wave. We find energy bands that are separated by gaps. The bands are characterized by a parameter $\theta$, which corresponds to the phase that the electron picks up when it tunnels from one minimum to another. Analogously, the real QCD ground state will be written as a Bloch wave and is equally characterized by a phase $\theta$. This phase is a new fundamental constant of nature and can be measured in experiments. However, so far, no experiment was able to measure $\theta$ for the QCD vacuum and we only know that it is incredibly small. In theory, the measurement is possible, because $\theta$ tells us to what extent strong interactions respect CP symmetry. The surprising smallness of $\theta$ is known as the strong CP problem. QCD alone says nothing about the value of $\theta$ and therefore it could be any number.
The QCD Vacuum Structure
The vacuum of a theory is defined as the state with the minimal amount of energy. In a non-abelian gauge theory, this minimal amount of energy can be defined to be zero and corresponds, for example, to the gauge potential configuration
$$ G_\mu = 0 . $$
However, this is not the only potential configuration with zero energy. Every gauge transformation of $0$ is also a state with minimal energy. The gauge potential transforms under gauge transformations $U$ as:
\begin{equation}
G_{\mu} \to U G_{\mu} U^\dagger -\frac{i}{g}U\partial_{\mu}U^{\dagger} .
\end{equation}
Putting $G_\mu = 0$ into this formula yields all configurations of the gauge potential with zero energy, i.e. all vacuum configurations:
\begin{equation}
G_{\mu}^{\left( pg\right) }=\frac{-i}{g}U\partial_{\mu}U^{\dagger}
\label{pureg}%
\end{equation}
Such configurations are called pure gauge.
This observation means that we have infinitely many possible field configurations with the minimal amount of energy. Each of these is a “classical” vacuum state of the theory. This may not seem very interesting because all these states are connected by a gauge transformation. Thus aren’t all these “classical” vacua equivalent? Isn’t there just one vacuum state that we can write in many complicated ways by using gauge transformations?
Well… to understand if things are really that simple, we need to talk about gauge transformations. Each “classical” vacuum of the theory corresponds to a specific gauge transformation $U$ via the formula
\begin{equation}
G_{\mu}^{\left( pg\right) }=\frac{-i}{g}U\partial_{\mu}U^{\dagger} .
\end{equation}
Now, the standard way to investigate the situation further is to mention the following two things as casually as possible
1.) We work in the temporal gauge $A_0 = 0$.
2.) We assume that it is sufficient to only consider those gauge transformations that become trivial at infinity $U(x) \to 1$ for $|x| \to \infty $.
Most textbooks and reviews offer at most one sentence to explain why we do these things. In fact, most authors act like assumptions are trivial and obvious or not important at all. As soon as these “nasty” technicalities are out of the way, we can start discussing the beautiful picture of the QCD vacuum that emerges under these assumptions. However, things aren’t really that simple. We will discuss the two assumptions in my second post about the QCD vacuum. Here I just note that they are not obvious choices and you need a very special perspective if you want to understand these choices.
For now, we simply summarize what we can say about our gauge transformations under these assumptions.
So, now back to the vacuum. We wanted to talk about gauge transformations, to understand if really all “classical” vacua are trivially equivalent.
We will see in a moment that the subset of all gauge transformations that fulfill the extra condition $U(x) \to 1$ for $|x| \to \infty $, fall into distinct subsets that can’t be smoothly transformed into each other. The interpretation of this observation is that these distinct subsets correspond via the formula $G_{\mu}^{\left( pg\right) }=\frac{-i}{g}U\partial_{\mu}U^{\dagger}$ to distinct vacua. In addition, when we investigate how a change from one such distinct vacuum configuration into another can happen, we notice that this is only possible if the field leaves the pure gauge configuration for a short amount of time. This is interpreted as a potential barrier between the distinct vacua.
How does this picture emerge? For simplicity, we consider $SU(2)$ instead of as $SU(3)$ as a gauge group, because the results are exactly the same.
“Actually it is sufficient to consider the gauge group $SU(2)$ since a general theorem states that for a Lie group containing $SU(2)$ as a subgroup the instantons are those of the $SU(2)$ subgroup.”
(page 863 in Quantum Field Theory and Critical Phenomena by Zinn-Justin)
Any element of $SU(2)$ can be written as
$$ U(x) = e^{i f(x) \vec{r} \vec{\sigma} },$$
where $\vec{\sigma}=(\sigma_1,\sigma_2,\sigma_3)$ are the usual Pauli matrices and $ \vec{r} $ is a unit vector. The condition $U(x) \to 1$ for $|x| \to \infty $ therefore means $f(x) \to 2\pi n$ for $|x| \to \infty $, where $n$ is an arbitrary integer, because we can write the matrix exponential as
$$e^{i f(x) \vec{r} \vec{\sigma}} = \cos(f(x)) + i \vec{r} \vec{\sigma} \sin( f(x) ) .$$
( $\sin( 2\pi n ) = 0 $ and $\cos(2\pi n ) =1 $ for an arbitrary integer $n$.)
The number $n$ that appears in the limit of the function $f(x)$ as we go to infinity, is called the winding number. (To confuse people there exist several other names: Topological charge, Pontryagin index, second Chern class number, …)
Before we discuss why this name makes sense, we need to talk about why we are interested in this number. To understand this, take note that we can’t transform a gauge potential configuration that corresponds to a gauge transformation with winding number $1$ (i.e. where the function $f(x)$ in the exponential approaches $2 \pi$ as we go to $|x| \to \infty$) into a gauge potential configuration that corresponds to a gauge transformation with a different winding number. In this sense, the corresponding vacuum configurations are distinct.
Similar sentences appears in all books and reviews and confused me a lot. An explicit example of a gauge transformation with winding number $1$ is
\begin{equation}
U^{\left( 1\right) }\left( \vec{x}\right) =\exp\left( \frac{i\pi
x^{a}\tau^{a}}{\sqrt{x^{2}+c^{2}}}\right)
\end{equation}
and a trivial example of a gauge transformation with winding number $0$ is
\begin{equation}
U^{\left( 0\right) }\left( \vec{x}\right) =1 .
\end{equation}
I can define
$$U^\lambda(\vec x) = \exp\left( \lambda \frac{i\pi
x^{a}\tau^{a}}{\sqrt{x^{2}+c^{2}}}\right) $$
and certainly
$$ U^{\lambda=0}(\vec x) = I $$
$$ U^{\lambda=1}(\vec x) = U^{\left( 1\right) }\left( \vec{x}\right) $$
Thus I have found a smooth map that transforms $U^{\left( 1\right) }\left( \vec{x}\right)$ into $U^{0}(\vec x)$.
The thing is that we restricted ourselves to only those gauge transformations that satisfy $U(x) \to 1$ for $|x| \to \infty $. For an arbitrary $\lambda$ this is certainly not the case. Thus, the correct statement is that we can’t transform $U^{0}(\vec x)$ to $U^{\left( 1\right) }\left( \vec{x}\right)$ without leaving the subset of gauge transformations that yield $U(x) \to 1$ for $|x| \to \infty $ . To transform $U^{\left( 1\right) }\left( \vec{x}\right)$ smoothly into $U^{0}(\vec x)$ requires gauge transformations that do not approach the identity transformation at infinity. (Smoothly means that we can invent a map which is smooth in some parameter $\lambda$ (as I did above in my definition of $U^\lambda(\vec x)$) that yields $U^{0}(\vec x)$ for $\lambda =0 $ and $U^{1}(\vec x)$ for $\lambda =1 $.)
Maybe a different perspective helps to understand this important point a little better. As mentioned above, a gauge transformation always involves the generator $G_a$ and some function $f(x)$ and can be written as $U(x)=e^{i f(x) \vec{r} \vec{\sigma}}$, where $\vec{r}$ is some unit vector. The generators are just matrices and therefore the restriction $U(x) \to 1 $ for $|x| \to \infty$ translated directly to $f(x) \to 2 \pi n$ for $|x| \to \infty$. The crucial thing is now that only these discrete endpoints are allowed for the functions that appear in the exponent of our gauge functions that satisfy $U(x) \to 1 $ for $|x| \to \infty$. If you now imagine some arbitrary function $f(x)$ that goes to $0$ and another function $g(x)$ that goes to $2 \pi$ at spatial infinity, it becomes clear that you can’t smoothly deform $f(x)$ into $g(x)$, while keeping the endpoint fixed at one of the allowed values! The crucial thing is really that we require that endpoint at spatial infinity of the functions that appear in the exponential are restricted to the values $2 \pi n$.
Maybe an (admittedly ugly) picture helps to bring this point home:
To summarize: by restricting ourselves to a subset of gauge transformations that approach $1$ at infinity, we’re able to classify the gauge transformations according to the number which the function in the exponent approaches. This number is called the winding number and gauge transformations with a different winding number cannot be smoothly transformed into each other without leaving our subset of gauge transformations.
So far, all we found is a method to label our gauge transformations. But what does this means for our classical vacua?
We can see explicitly that two vacuum configurations that correspond to gauge transformations with a different winding number are separated by a potential barrier. This observation will mean that our infinitely many vacuum states do not lie next to each other (not meant in a spatial sense). Instead, there is a potential barrier between them.
(Afterwards, we will talk about the so-far a bit unmotivated name “winding number”.)
Origin of the Potential Barrier between Vacua
So we start with a gauge potential $A_i^{(1)}(x)$ that is generated by a gauge transformation that belongs, say, to the equivalence class with the winding number $1$. We want to describe the change of this gauge potential to the gauge potential that is generated by a gauge transformation of winding number $0$, which simply means $A_i^{(0)}=0$. A possible description is
$$ A_i^{(\beta)}(x) = \beta A_i^{(1)}(x) $$
where $\beta$ is a real parameter. For $\beta =0$, we get the gauge potential with winding number $0$: $A_i^{(0)}=0$, and for $\beta =1$, we get the gauge potential with winding number $1$:$A_i^{(1)}(x) $.
For $\beta =1$ and $\beta =0$ our $A_i^{(\beta)}(x)$ corresponds to zero classical energy, because we are dealing with a pure gauge potentials.
However, for any other value for $\beta$ in between: $0<\beta <1$, our $A_i^{(\beta)}(x)$ is not pure gauge!
The analogue of the electric field for a non-abelian gauge theory $E_i \equiv G^{0i}$ still vanishes, because$\dot{A}_i^{(\beta)}=0$ and $A_i^{(\beta)}(x)$ are time-independent. In contrast, the analogue of the magnetic field $V_i \equiv \frac{1}{2} \epsilon{ijk}G^{jk}$ does not vanish:
\begin{align} G_{jk} &= \beta(\partial_j A_k^{(1)}-\partial_k A_j^{(1)} + \beta^2 [A_j^{(1)},A_k^{(1)} ] \notag \\
&=(\beta^2-\beta)[A_j^{(1)},A_k^{(1)} ] \notag \\
& \neq 0 \quad \text{ for } 0 <\beta < 1.
\end{align}
The energy is proportional to $\int Tr(G_{jk}G_{jk})d^3x$, and is therefore non-zero for $0< \beta < 1$. It is important to notice that it not only non-zero, but also finite. This is, because at the boundaries $A_k^{(1)}$ vanishes sufficiently fast.
To summarize: $A_i^{(\beta)}(x)$ describes the transition from a vacuum state with winding number $1$ to a vacuum state with winding number $0$. By considering the field energy $\int Tr(G_{jk}G_{jk})d^3x$, explicitly, we can see that during this transition the field does not stay in a pure gauge transformation all the time. Instead, during the transition from $A_i^{(1)}(x) $ to $A_i^{(0)}(x) $ we necessarily encounter field configurations that correspond to a non-zero, but finite, field energy. In this sense, we can say that there is a finite potential barrier between vacua with a different winding number.
What is a winding number?
In the previous sections, we simply used the notion “winding number”. This notion is best understood by considering an easy example with $U(1)$ as a gauge group. In addition, to make things even more simple, we restrict ourselves to only one spatial dimension. Afterward, we will talk about the notion winding number in the $SU(2)$ and 4D context that we are really interested here.
Winding Number for a U(1) gauge theory
As a reminder: We are interested in gauge transformations that yield physical gauge field configurations through
\begin{equation}
G_{\mu}^{\left( pg\right) }=\frac{-i}{g(x)}U\partial_{\mu}U^{\dagger}
\end{equation}
Thus, we assume that our $g(x)$ behave nicely everywhere. Especially this means that $g(x)$ must be a continuous function because otherwise, we would have points with infinite field momentum. The reason for this is that the field momentum is directly related to the derivative of the field with respect to $x$ and if there is a non-continuous jump somewhere, the derivative of the field would be infinity there.
As casually mentioned above (and as will be discussed below), we restrict ourselves to those gauge transformations $U(x)$ that satisfy $U(x) \to 1 $ for $|x| \to \infty$. This condition means that we are allowed to consider the range where $x$ is defined as an element of $S^1$ instead of as an element of $\mathbb{R}$. The reason for this is $U(x) \to 1 $ for $|x| \to \infty$ means that $U(x)$ has the same value at $x= – \infty$ and at $x= \infty$. Since all that interests us here is $U(x)$ or functions that are derived from $U(x)$, we can use instead of two points $-\infty$ and $\infty$, just one point, the point at infinity. Expressed differently, because of the condition $U(x) \to 1 $ for $|x| \to \infty$ we can treat $x= -\infty$ and $x = \infty$ as one point and this means our $\mathbb{R}$ becomes a circle $S^1$:
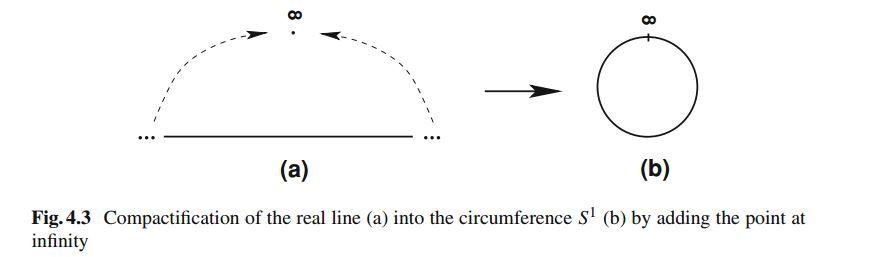
source: http://www.iop.vast.ac.vn/theor/conferences/vsop/18/files/QFT-4.pdf
Here’s the same procedure for 3 dimensions:
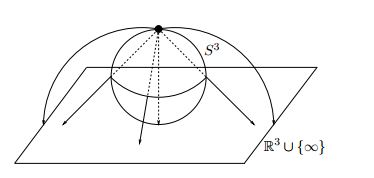
Source: https://arxiv.org/pdf/hep-th/0010225.pdf
Therefore, our gauge transformations are no longer functions that eat an element of $\mathbb{R}$ and spit out an element of the gauge group $U(1)$, but instead they are now maps from the circle $S^1$ to $U(1)$. Points on the circle can be parameterized by an angle $\phi$ that runs from $0$ to $2\pi$ and therefore, we can write possible maps as follows:
$$ S^1 \to U(1) : g(\phi)= e^{i\alpha(\phi)} \, . $$
A key observation is now that the set of all possible $g(\phi)$ is divided into various topological sectors, which can be labeled by an integer $n$. This can be understood as follows:
The map from the circle $S^1$ to $U(1)$ needs not to be one-to-one. The degree to which a given map is not one-to-one is the winding number. For example, when the map is two-to-one, the winding number is 2. A map from the circle onto elements of $U(1)$ is
$$ S^1 \to U(1) : f_n(\phi)= e^{in\phi} \, . $$
This map eats elements of the circle $S^1$ and spits out a $U(1)$. Now, depending on the value of $n$ in the exponent we get for multiple elements of the circle the same $U(1)$ element.
Here is how we can think about a map with winding number 1:
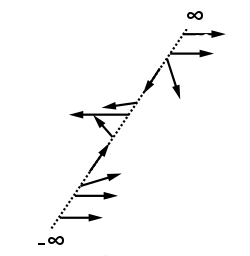
(For simplicity, space is here depicted as a line instead of a circle. Just imagine that the endpoints ∞ and -∞ are identified.)
Each arrow that points in a different direction stands for a different $U(1)$ element. As we move from ∞ to -∞ we encounter each $U(1)$ element exactly once. Similarly, a gauge transformation with winding number $0$ would only consist of arrows that point upwards, i.e. each element is mapped to the same $U(1)$ element, namely the identity. A gauge transformation with winding number 2 would consist of arrows that rotate twice as we move from ∞ to -∞, and so on for higher winding numbers.
Formulated differently, this means that depending on $n$ our map $f_n(\phi)$ maps several points on the circle onto the same $U(1)$ element.
For example, if $n=2$, we have
$$ f_2(\phi)= e^{i2\phi} .$$
Therefore
$$ f_2(\pi/2)= e^{i \pi} = -1 $$
and also
$$ f_2(3\pi/2)= e^{i3 \pi} = e^{i2 \pi} e^{i1 \pi} = -1 .$$
Therefore, as promised, for $n=2$ the map is two-to-one, because $\phi=\pi/2$ and $\phi= 3\pi/2$ are mapped onto the same $U(1)$ element. Equally, for $n=3$, we get for $\phi=\pi/3$, $\phi=\pi$ and $\phi= 5\pi/3$ the same $U(1)$ element $f_3(\pi/3)=f_3(\pi)=f_3(5\pi/3)=-1$.
In this sense, the map $f_n(\phi)$ determines how often $U(1)$ is wrapped around the circle and this justifies the name “winding number” for the number $n$.
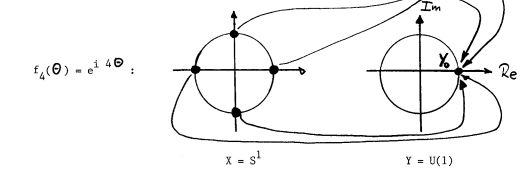
Source: page 80 Selected Topics in Gauge Theories by Walter Dittrich, Martin Reuter
As a side remark: The elements of $U(1)$ also lie on a circle in the complex plane. ($U(1)$ is the group of the unit complex numbers). Thus, in this sense, $f_n(\phi)$ is a map from $S^1 \to S^1$.
A clever way to extract the winding number for an arbitrary map $ S^1 \to U(1)$ is to compute the following integral
$$ \int_0^{2\pi} d\phi \frac{f_n'(\phi)}{f_n(\phi)} = 2\pi i n, $$
where $f_n'(\phi)$ is the derivative of $f_n(\phi)$. Such tricks are useful for more complicated structures where the winding number isn’t that obvious.
Winding Number for an SU(2) gauge theory
Now, analogous to the compactification of $\mathbb{R}$ to the circle $S^1$, we compactify our three space dimensions to the three-sphere $S^3$. The argument is again the same, that the restriction $U(x) \to 1 $ for $|x| \to \infty$ means that spatial infinity looks everywhere the same, no matter how we approached it (i.e. from all directions). Thus there is just one point infinity and not, for example, the edges of a hyperplane as infinities.
Thus, for a $SU(2)$ gauge theory our gauge transformations are maps from $S^3$ to $SU(2)$. In addition, completely analogous to how we can understand $U(1)$, i.e. the set of unit complex numbers, as the circle $S^1$, we can understand $SU(2)$, the set of unit quaternions, as a sphere $S^3$. Thus, in some sense our gauge transformations, are maps
$$ S^3 \to S^3 \quad : \quad U(x) = a_0(x) 1 + i a_i(x) \sigma ,$$
where $\sigma$ are the Pauli matrices.
Again, we can divide the set of all $SU(2)$ gauge transformations into topological distinct sets that are labeled by an integer.
Analogous to how we could extract the $U(1)$ winding number from a given gauge transformation, we can compute the $SU(2)$ winding number by using an integral formula (source: page 23 here):
$$n = \frac{1}{24\pi^2} \int_{S^3} d^3x \epsilon_{ijk} Tr\left[ \left( U^{-1} \partial_i U \right)\left(U^{-1} \partial_jU \right)\left(U^{-1} \partial_kU \right) \right] $$
This formula looks incredibly complicated, but can be understood quite easily. The trick is that we can parametrize elements of $SU(2)$ by Euler angles $\alpha,\beta,\gamma$ and then define a volume element in parameter space
$$ d\mu(U) = \frac{1}{16\pi} \sin\beta d\alpha d\beta d\gamma . $$
Then by an explicit computation one can show that this volume element can be expressed as
$$d\mu(U) = \frac{1}{4\pi} Tr\left[ \left( U^{-1} \partial_i U \right)\left(U^{-1} \partial_jU \right)\left(U^{-1} \partial_kU \right) \right]d\alpha d\beta d\gamma .$$
This allows us to see that the integral over this volume element yields indeed, when we integrate $x$ all over the spatial $S^3$, the number of times we get the $SU(2)$ manifold. Moreover, geometrically $SU(2)$ is $S^3$, too. Expressed differently, when $x$ ranges one time over all points on the spatial sphere $S^3$, the winding number integral is simply the integral over the volume element of $SU(2)$ and yields the number of times we get the $SU(2)$ manifold. For example, when we have the trivial gauge function
$$U=1 ,$$
we cover the $SU(2)$ sphere zero times.
However, for example, for
$$ U^{(1)}(x) = \frac{1}{|x|}(x_4+ \vec x \cdot \vec \sigma)$$
we can see that we get exactly one time all the points of a sphere $S^3$, when the $x$ range one time over all points on the spatial $S^3$. Thus this gauge transformation has winding number $1$.
Gauge transformations with an arbitrary winding number can be computed from the gauge transformation with winding number $1$ via
$$ U(x)^{(n)} = [U^{(1)}(x)]^n $$
All this is shown nicely and explicitly on page 90 in the second edition of Quarks, Leptons and Gauge Fields by Kerson Huang. He also shows explicitly why $ U(x)^{(n)} = [U)^{(1)}(x)]^n $ holds.
Now it’s probably time for a short intermediate summary.
Intermediate Summary – What have we learned so far?
We started by studying vacuum configurations of Yang-Mills field theory (a gauge theory, for example, with $SU(3)$ gauge symmetry like QCD). Vacuum configurations correspond to field configurations with a minimal amount of field energy. This means they correspond to vanishing field strength tensors and thus to gauge potential configurations that are pure gauge:
$$A_\mu = U \partial_\mu (U^{-1}) .$$
We then made two assumptions. While the first assumption (temporal gauge $A_0 = 0$) look okay, the second one is really strange: We restrict ourselves to those gauge transformations that satisfy the condition $U(x) \to 1$ for $|x| \to \infty$. Just to emphasize how strange this assumption is, here is a picture:
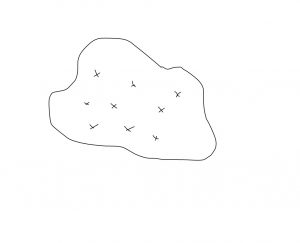
Imagine this geometrical objects represents all gauge transformations, i.e. each point is a gauge transformation. What we do with the restriction $U(x) \to 1$ for $|x| \to \infty$ is cherry picking. We pick from this huge set only a very specific set of gauge transformations, denoted by $X$’s in the picture. With this in mind, it’s no wonder that the resulting topology is non-trivial.
However, without discussing this assumption any further we pushed on and discussed the picture of the vacuum that emerges from these assumptions.
We found that the subset of all gauge configurations that satisfy $U(x) \to 1$ for $|x| \to \infty$ can be classified with the help of a label called winding number. We then computed that if the gauge potential changes from one vacuum configuration with a given winding number to a configuration with a different winding number, it needs to go through configurations that correspond to a non-zero field energy. This means that there is a potential barrier between configurations with a different winding number.
We then talked about why the name “winding number” makes sense. The crucial point is that this number really measures how often the gauge group winds around spacetime.
Physical Implications of the Periodic Structure
The first ones who came up with the periodic picture of the QCD vacuum that we described above, were Jackiw and Rebbi in 1976. However, they didn’t simply looked at QCD and then derived this structure.
Instead, they a had a very specific goal when they started their analysis. Their study was motivated by the recent discovery of so-called instantons (Alexander Belavin, Alexander Polyakov, Albert Schwarz and Yu. S. Tyupkin 1975).
Instantons are finite energy solutions of the Yang-Mills equations in Euclidean spacetime. For reasons that will be explained in a second post, this leads to the suspicion that they have something to do with tunneling processes.
(In short: The transformation from Minkowski to Euclidean spacetime is $t \to i \tau$. A “normal” wave function in quantum mechanics looks like $\Psi \sim e^{iEt}$. Now, remember how the quantum mechanical solution looks like for the tunneling of a particle through a potential barrier $\Psi \sim e^{-Et}$. The difference is $t \to i \tau$, too! This is the main reason why normal solutions in Euclidean spacetime are considered to be tunneling solutions in Minkowski spacetime.)
The motivation behind the study by Jackiw and Rebbi was to make sense of these instanton solutions in physical terms. What is tunneling? And from where to where?
(While you may not care about the history of physics, this bit of history is crucial to understand the paper by Jackiw and Rebbi; and especially how the standard picture of the QCD vacuum came about. The important thing to keep in mind is that instantons were discovered before the periodic structure of the QCD vacuum. )
The notion “winding number” was already used by Belavin, Polyakov, Schwarz, and Tyupkin. However, no physical interpretation was given. The idea by Jackiw and Rebbi was that instantons describe the tunneling between vacuum states that carry different winding number. Most importantly, they had the idea that vacuum states with different integer winding number are separated by a potential barrier, as already discussed above. Thus, the vacuum states do not lie “next to each other” and the quantum field can only transform itself from one such vacuum state into another through a tunneling process (or, of course, if it carries enough energy, for example, when the temperature is high enough).
The situation then is completely analogous to an electron in a crystal. The crystal is responsible for a periodic structure in which the electron “moves”. Like the QCD gauge field, the electron needs to tunnel to get from one minimum in the crystal potential to the next. Let’s say the minima of the crystal potential are separated by a distance $a$. Then, we can conclude that the periodic structure of the potential means that the wave function must be periodic, too: $\psi(x) = \psi(x+a)$! However, we are dealing with quantum mechanical wave functions and thus, it’s possible that the electron picks up a phase when it tunnels from one minimum to the next: $\psi(x) = e^{i\theta} \psi(x+a)$! This makes no difference for the conclusion that the probability to find the electron must be the same for locations that are separated by the distance $a$. The correct states of the electron are then not described by some $\psi(x)$, but rather by a superposition of the wave function of all minima. There are different superpositions possible, and each one is characterized by a specific value of the phase parameter $\theta$. The resulting wave function is known as Bloch wave and the phase $\theta$ as Bloch momentum. (You can read much more on this, for example in Kittel chapter 9 and Ashcroft-Mermin chapter 8).
The idea of Jackiw and Rebbi was that we have exactly the same situation for the QCD vacuum.
We have a periodic potential, tunneling between the minimas, and consequently also a parameter $\theta$, analogous to the Bloch momentum. (Take note that for the QCD vacuum neighboring minima are not separated by some distance $a$, but instead by a winding number difference of $1$.) Upon closer inspection, it turns out that the parameter $\theta$ leads to CP violation in QCD interactions and can, in principle, be measured.
It is important to know the backstory of the paper by Jackiw and Rebbi because otherwise some of their arguments do not seem to make much sense. They already knew about the instanton solutions and had the “electron in a crystal” picture in mind as a physical interpretation of the instantons. Around this idea, they wrote their paper.
The periodic vacuum structure of the QCD vacuum was not discovered from scratch, but with these very specific ideas in mind.
We have seen above, that the periodic structure of the QCD vacuum does not arise without two crucial assumptions. If you know that this structure was first described with instantons and Bloch waves in mind, it makes a lot more sense how the original authors came up with these assumptions. These assumptions are exactly what you need to give the QCD vacuum the nice periodic structure and thus to be able to draw the analogy with an electron in a crystal. As I will describe in a later post, without these assumptions, the QCD vacuum looks very different.
In their original paper, Jackiw and Rebbi motivated one of the assumptions, namely the restriction to gauge transformations that satisfy $g(x) \to 1$ for $|x| \to \infty$, simply with “we study effects which are local in space and therefore”. As far as I know, this reason does not make sense and was never again repeated in any later paper. In subsequent papers, Jackiw came up with all sorts of different reasons for this restriction. However, ultimately in 1980, he concluded: “while some plausible arguments can be given in support of this hypothesis (see below) in the end we must recognize it as an assumption” (Source).
The path to the standard periodic picture of the QCD vacuum was thus not through some rigorous analyses, but rather strongly guided by “physical intuition”. It was the idea, that the interpretation of the QCD vacuum could be done similar to the quantum mechanical problem of an electron in a crystal, which lead to the periodic picture of the QCD vacuum.
My point is not that this picture is wrong. Instead, I was long puzzled for along time by the reasons that are given for the restriction $g(x) \to 1$ for $|x| \to \infty$ and I want to help others who are confused by them, too. I will write a lot more about this in a second post, but I hope that the few paragraphs above already help a bit. The path to the periodic vacuum structure is not as straight-forward as most authors want you to believe. However, it is important to keep in mind that only because physicists came up with a description through intuition and not via some rigorous analysis, does not mean that it is wrong. Even when the original arguments the discoverers give do not hold upon closer scrutiny, it is still possible that their conclusions are correct. As already mentioned above, after the original publication, both Jackiw and Rebbi and many other authors, came up with lots of other arguments to strengthen the case for the periodic vacuum picture.
However, it is also important to keep in mind that, so far, all experimental evidence point in the direction that $\theta$ is tiny $\theta \lesssim 10^{10}$ or even zero. This is hard to understand if you believe in the analogy with the Bloch wave. In this picture, $\theta$ is an arbitrary phase and could be any value between $0$ and $2\pi$. There is no reason why it should be so tiny or even zero. This is famously known as the strong CP problem. (Things aren’t really that simple. The parameter $\theta$ also pops up from a completely different direction, namely from an analysis of the chiral anomaly. Thus, even if you don’t believe in the Bloch wave picture of the QCD vacuum, you end up with a $\theta$ parameter. Much more on this in a later post.)
Outlook (or: which puzzle pieces are still missing?)
Unfortunately, there are still a lot of loose ends. These will be hopefully tied up in future posts.
Most importantly we need to talk more about the assumptions
1.) The choice of the temporal gauge $A_0 = 0$.
2.) The restriction to those gauge transformations that become trivial at infinity $U(x) \to 1$ for $|x| \to \infty $.
In the second post of this series, I will try to elucidate these assumptions which are only noted in passing in almost all standard discussion of the QCD vacuum.
In a third post, I will show how the QCD vacuum can be understood beautifully from a completely different perspective.
Another important loose end is that we have not talked about instantons so far. These are solutions of the Yang-Mills equations and describe the tunneling processes between degenerate vacua.
Until I have finished these posts, here are some reading recommendations.
Reading Recommendations
The classical papers that elucidated the standard picture of the QCD vacuum are:
- Vacuum Periodicity in a Yang-Mills Quantum Theory by R. Jackiw and C. Rebbi
- Toward a theory of the strong interactions by Curtis G. Callan, Jr., Roger Dashen, and David J. Gross
- The Structure of the Gauge Theory Vacuum Curtis G. Callan et. al.
- Pseudoparticle solutions of the Yang-Mills equations A.A. Belavin et. al.
- Concept of Nonintegrable Phase Factors and Global Formulation of Gauge Fields Tai Tsun Wu (Harvard U.), Chen Ning Yang
The standard introductions to instantons and the QCD vacuum are:
- ABC of instantons by A I Vaĭnshteĭn, Valentin I Zakharov, Viktor A Novikov and Mikhail A Shifman
- The Uses of Instantons by Sidney Coleman
(However, I found them both to be not very helpful)
Books on the topic are:
- The QCD Vacuum, Hadrons and Superdense Matter by E. V. Shuryak
- Solitons and Instantons by Ramamurti Rajaraman (Highly Recommended)
- Classical Solutions in Quantum Field Theory: Solitons and Instantons by Erick Weinberg
- Topological Solitons by Manton and Sutcliff (Highly Recommended)
- Some Elementary Gauge Theory Concepts Hong-Mo Chan, Sheung Tsun Tsou
- Classical Theory of Gauge Fields by Rubakov (Highly Recommended)
Review articles are:
- Theory and phenomenology of the QCD vacuum by Edward V. Shuryak
- A Primer on Instantons in QCD by Hilmar Forkel (Highly Recommended)
- Effects of Topological Charge in Gauge Theories R.J. Crewther
- TASI Lectures on Solitons Instantons, Monopoles, Vortices and Kinks David Tong
- Topological Concepts in Gauge Theories by F. Lenz
Textbooks that contain helpful chapters on instantons and the QCD vacuum are:
- Quarks, Leptons & Gauge Fields by Kerson Huang (Highly Recommended)
- Quantum Field Theory by Lewis H. Ryder (Highly Recommended)
- Quantum Field Theory by Mark Srednicki (Highly Recommended)
- Quantum Field Theory and Critical Phenomena by Zinn-Justin
Another informal introduction is:
- ’t Hooft and η’ail Instantons and their applications by Flip Tanedo
The same things explained more mathematically can be found in:
- Geometry of Yang-Mills Fields by M. F. ATIYAH
- plus chapters in Geometry of Physics by Frankel and
- Topology and Geometry for Physicists by Nash and Sen